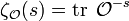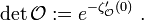Zeta function (operator)

The zeta function of a mathematical operator 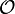$\mathcal O$ is a function defined as

\zeta_{\mathcal O}(s) = \operatorname{tr} \; \mathcal O^{-s}

for those values of s where this expression exists, and as an analytic continuation of this function for other values of s. Here "tr" denotes a functional trace.

The zeta function may also be expressible as a spectral zeta function^[1] in terms of the eigenvalues 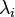$\lambda_i$ of the operator 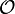$\mathcal O$ by

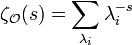\zeta_{\mathcal O}(s) = \sum_{\lambda_i} \lambda_i^{-s}

It is used in giving a rigorous definition to the functional determinant of an operator, which is given by

\det \mathcal O := e^{-\zeta'_{\mathcal O}(0)} \;.

The Minakshisundaram–Pleijel zeta function is an example, when the operator is the Laplacian of a compact Riemannian manifold.

One of the most important motivations for Arakelov theory is the zeta functions for operators with the method of heat kernels generalized algebro-geometrically.^[2]

References

↑ Lapidus & van Frankenhuijsen (2006) p.23
↑ Soulé, C.; with the collaboration of D. Abramovich, J.-F. Burnol and J. Kramer (1992), Lectures on Arakelov geometry, Cambridge Studies in Advanced Mathematics 33, Cambridge: Cambridge University Press, pp. viii+177, ISBN 0-521-41669-8, MR 1208731

Lapidus, Michel L.; van Frankenhuijsen, Machiel (2006), Fractal geometry, complex dimensions and zeta functions. Geometry and spectra of fractal strings, Springer Monographs in Mathematics, New York, NY: Springer-Verlag, ISBN 0-387-33285-5, Zbl 1119.28005
Fursaev, Dmitri; Vassilevich, Dmitri (2011), Operators, Geometry and Quanta: Methods of Spectral Geometry in Quantum Field Theory, Theoretical and Mathematical Physics, Springer-Verlag, p. 98, ISBN 94-007-0204-3