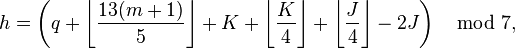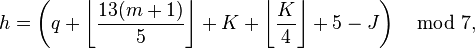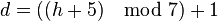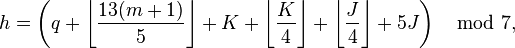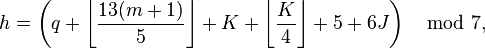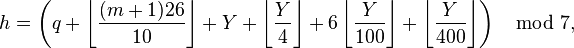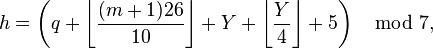Zeller's congruence

Zeller's congruence is an algorithm devised by Christian Zeller to calculate the day of the week for any Julian or Gregorian calendar date. It can be considered to be based on the conversion between Julian day and the calendar date.

Formula

For the Gregorian calendar, Zeller's congruence is

h = \left(q + \left\lfloor\frac{13(m+1)}{5}\right\rfloor + K + \left\lfloor\frac{K}{4}\right\rfloor + \left\lfloor\frac{J}{4}\right\rfloor - 2J\right) \mod 7,

for the Julian calendar it is

h = \left(q + \left\lfloor\frac{13(m+1)}{5}\right\rfloor + K + \left\lfloor\frac{K}{4}\right\rfloor + 5 - J\right) \mod 7,

where

h is the day of the week (0 = Saturday, 1 = Sunday, 2 = Monday, ..., 6 = Friday)
q is the day of the month
m is the month (3 = March, 4 = April, 5 = May, ..., 14 = February)
K the year of the century ( $year \mod 100$ ).
J is the zero-based century (actually 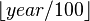$\lfloor year/100 \rfloor$ ) For example, the zero-based centuries for 1995 and 2000 are 19 and 20 respectively (to not be confused with the common ordinal century enumeration which indicates 20th for both cases).

NOTE: In this algorithm January and February are counted as months 13 and 14 of the previous year. E.g. if it is 2 February 2010, the algorithm counts the date as the second day of the fourteenth month of 2009 (02/14/2009 in DD/MM/YYYY format)

For an ISO week date Day-of-Week d (1 = Monday to 7 = Sunday), use

d = ((h + 5) \mod 7) + 1

Implementation in software

The formulas rely on the mathematician's definition of modulo division, which means that −2 mod 7 is equal to positive 5. Unfortunately, the way most computer languages implement the remainder function, −2 mod 7 returns a result of −2. So, to implement Zeller's congruence on a computer, the formulas should be altered slightly to ensure a positive numerator. The simplest way to do this is to replace $- 2 J$ by $+ 5 J$ and $- J$ by $+ 6 J$ . So the formulas become:

h = \left(q + \left\lfloor\frac{13(m+1)}{5}\right\rfloor + K + \left\lfloor\frac{K}{4}\right\rfloor + \left\lfloor\frac{J}{4}\right\rfloor + 5J\right) \mod 7,

for the Gregorian calendar, and

h = \left(q + \left\lfloor\frac{13(m+1)}{5}\right\rfloor + K + \left\lfloor\frac{K}{4}\right\rfloor + 5 + 6J\right) \mod 7,

for the Julian calendar.

One can readily see that, in a given year, March 1 (if that is a Saturday, then March 2) is a good test date; and that, in a given century, the best test year is that which is a multiple of 100.

Zeller used decimal arithmetic, and found it convenient to use J and K in representing the year. But when using a computer, it is simpler to handle the modified year $Y$ , which is $Y - 1$ during January and February:

h = \left(q + \left\lfloor\frac{(m+1)26}{10}\right\rfloor + Y + \left\lfloor\frac{Y}{4}\right\rfloor + 6\left\lfloor\frac{Y}{100}\right\rfloor + \left\lfloor\frac{Y}{400}\right\rfloor\right) \mod 7,

for the Gregorian calendar, and

h = \left(q + \left\lfloor\frac{(m+1)26}{10}\right\rfloor + Y + \left\lfloor\frac{Y}{4}\right\rfloor + 5\right) \mod 7,

for the Julian calendar.

Analysis

These formulas are based on the observation that the day of the week progresses in a predictable manner based upon each subpart of that date. Each term within the formula is used to calculate the offset needed to obtain the correct day of the week.

For the Gregorian calendar, the various parts of this formula can therefore be understood as follows:

$q$ represents the progression of the day of the week based on the day of the month, since each successive day results in an additional offset of 1 in the day of the week.

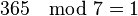$K$ represents the progression of the day of the week based on the year. Assuming that each year is 365 days long, the same date on each succeeding year will be offset by a value of $365\mod 7 = 1$ .

Since there are 366 days in each leap year, this needs to be accounted for by adding another day to the day of the week offset value. This is accomplished by adding 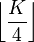$\left\lfloor\frac{K}{4}\right\rfloor$ to the offset. This term is calculated as an integer result. Any remainder is discarded.

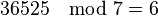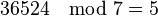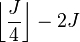Using similar logic, the progression of the day of the week for each century may be calculated by observing that there are 36524 days in a normal century and 36525 days in each century divisible by 400. Since $36525\mod 7 = 6$ and $36524\mod 7 = 5$ , the term : $\left\lfloor\frac{J}{4}\right\rfloor - 2J$ accounts for this (again using integer division and discarding any fractional remainder). To avoid negative numbers, this term can be replaced with : 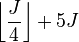$\left\lfloor\frac{J}{4}\right\rfloor + 5J$ with equivalent results.

The term 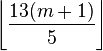$\left\lfloor\frac{13(m+1)}{5}\right\rfloor$ adjusts for the variation in the days of the month. Starting from January, the days in a month are {31, 28/29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31}. February's 28 or 29 days is a problem, so the formula rolls January and February around to the end so February's short count will not cause a problem. The formula is interested in days of the week, so the numbers in the sequence can be taken modulo 7. Then the number of days in a month modulo 7 (still starting with January) would be {3, 0/1, 3, 2, 3, 2, 3, 3, 2, 3, 2, 3}. Starting in March, the sequence basically alternates 3, 2, 3, 2, 3, but every five months there are two 31-day months in a row (July-August and December-January).^[1] The fraction 13/5 = 2.6 and the floor function have that effect; the denominator of 5 sets a period of 5 months.

The overall function, 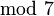$\mod 7$ , normalizes the result to reside in the range of 0 to 6, which yields the index of the correct day of the week for the date being analyzed.

The reason that the formula differs for the Julian calendar is that this calendar does not have a separate rule for leap centuries and is offset from the Gregorian calendar by a fixed number of days each century.

Since the Gregorian calendar was adopted at different times in different regions of the world, the location of an event is significant in determining the correct day of the week for a date that occurred during this transition period. This is only required through 1929, as this was the last year that the Julian calendar was still in use by any country on earth, and thus is not required for 1930 or later.

The formulae can be used proleptically, but with care for years before Year 0. To accommodate this, one can add a sufficient multiple of 400 Gregorian or 28 Julian years.

Examples

For 1 January 2000, the date would be treated as the 13th month of 1999, so the values would be:

q = 1

m = 13

K = 99

J = 19

So the formula evaluates as (1 + 36 + 99 + 24 + 4 − 38) mod 7 = 126 mod 7 = 0 = Saturday

(The 36 comes from (13+1)*26/10 = 364/10, truncated to an integer.)

However, for 1 March 2000, the date is treated as the 3rd month of 2000, so the values become

q = 1

m = 3

K = 0

J = 20

so the formula evaluates as (1 + 10 + 0 + 0 + 5 − 40) mod 7 = −24 mod 7 = 4 = Wednesday

References

↑ The every five months rule only applies to the twelve months of a year.

Each of these four similar imaged papers deals firstly with the day of the week and secondly with the date of Easter Sunday, for the Julian and Gregorian Calendars. The pages link to translations into English.

Zeller, Christian (1882). "Die Grundaufgaben der Kalenderrechnung auf neue und vereinfachte Weise gelöst". Württembergische Vierteljahrshefte für Landesgeschichte (in German) V: 313–314.
Zeller, Christian (1883). "Problema duplex Calendarii fundamentale". Bulletin de la Société Mathématique de France (in Latin) 11: 59–61.
Zeller, Christian (1885). "Kalender-Formeln". Mathematisch-naturwissenschaftliche Mitteilungen des mathematisch-naturwissenschaftlichen Vereins in Württemberg (in German) 1 (1): 54–58.
Zeller, Christian (1886). "Kalender-Formeln". Acta Mathematica (in German) 9: 131–136. doi:10.1007/BF02406733.

External links

The Calendrical Works of Rektor Chr. Zeller: The Day-of-Week and Easter Formulae by J R Stockton, near London, UK. The site includes images and translations of the above four papers, and of Zeller's reference card "Das Ganze der Kalender-Rechnung".
Black, Paul E. "Zeller's congruence". Dictionary of Algorithms and Data Structures. NIST.