Zanstra method
The Zanstra method is a method to determine the temperature of central stars of planetary nebula. It was developed by Herman Zanstra in 1927.
It is assumed that the nebula is optically thick in the Lyman continuum which means that all ionizing photons from the central star are absorbed inside the nebula. Based on this assumption, the intensity ratio of a stellar reference frequency to a nebula line such as Hβ can be used to determine the central star's effective temperature.
.jpg)
Credit: NASA, ESA, and C.R. O'Dell (Vanderbilt University)
Zanstra method for a nebula of hydrogen
For a pure hydrogen nebula, the ionization equilibrium states that the number per unit time of ionizing photons from the central star has to be balanced by the rate of recombinations of protons and electrons to neutral hydrogen inside the Strömgren sphere of the nebula. Ionizations can only be caused by photons having at least the frequency 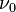 , corresponding to the ionization potential of hydrogen which is 13.6eV:
, corresponding to the ionization potential of hydrogen which is 13.6eV:
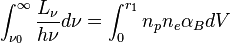
Here, 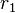 is the radius of the Strömgren sphere and
is the radius of the Strömgren sphere and 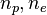 are the number densities of protons and electrons, respectively. The luminosity of the central star is denoted by
are the number densities of protons and electrons, respectively. The luminosity of the central star is denoted by 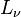 and
and 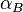 is the recombination coefficient to the excited levels of hydrogen.
is the recombination coefficient to the excited levels of hydrogen.
The ratio between the number of photons emitted by the nebula in the Hβ line and the number of ionizing photons from the central star can then be estimated:
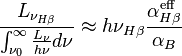
where 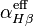 is the effective recombination coefficient for Hβ.
is the effective recombination coefficient for Hβ.
Given a stellar reference frequency  , the Zanstra ratio is defined by
, the Zanstra ratio is defined by
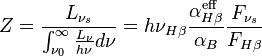
with 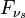 and
and 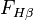 being the fluxes in the stellar reference frequency and in Hβ, respectively. Using the second formula, the Zanstra ratio can be determined by observations.
On the other hand, applying model stellar atmospheres, theoretical Zanstra ratios may be computed in dependence of the central star's effective temperature which may be fixed by comparison with the observed value of the Zanstra ratio.
being the fluxes in the stellar reference frequency and in Hβ, respectively. Using the second formula, the Zanstra ratio can be determined by observations.
On the other hand, applying model stellar atmospheres, theoretical Zanstra ratios may be computed in dependence of the central star's effective temperature which may be fixed by comparison with the observed value of the Zanstra ratio.
References
- Kwok, Sun (2000), The Origin and Evolution of Planetary Nebulae, Cambridge University Press
- Osterbrock, Donald E. (1989), Astrophysics of Gaseous Nebulae and Active Galactic Nuclei, University Science Books