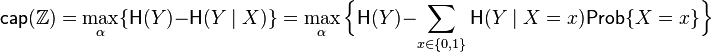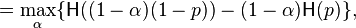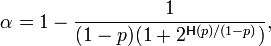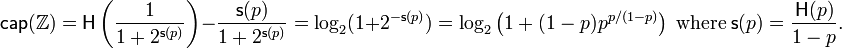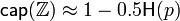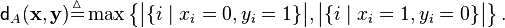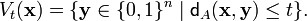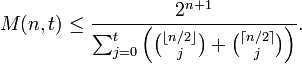Z-channel (information theory)
A Z-channel is a communications channel used in coding theory and information theory to model the behaviour of some data storage systems.
Definition
A Z-channel (or a binary asymmetric channel) is a channel with binary input and binary output where the crossover 1 → 0 occurs with nonnegative probability p, whereas the crossover 0 → 1 never occurs. In other words, if X and Y are the random variables describing the probability distributions of the input and the output of the channel, respectively, then the crossovers of the channel are characterized by the conditional probabilities
- Prob{Y = 0 | X = 0} = 1
- Prob{Y = 0 | X = 1} = p
- Prob{Y = 1 | X = 0} = 0
- Prob{Y = 1 | X = 1} = 1−p
Capacity
The capacity 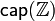 of the Z-channel
of the Z-channel  with the crossover 1 → 0 probability p, when the input random variable X is distributed according to the Bernoulli distribution with probability α for the occurrence of 0, is calculated as follows.
with the crossover 1 → 0 probability p, when the input random variable X is distributed according to the Bernoulli distribution with probability α for the occurrence of 0, is calculated as follows.
where 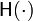 is the binary entropy function.
is the binary entropy function.
The maximum is attained for
yielding the following value of  as a function of p
as a function of p
For small p, the capacity is approximated by
as compared to the capacity 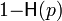 of the binary symmetric channel with crossover probability p.
of the binary symmetric channel with crossover probability p.
Bounds on the size of an asymmetric-error-correcting code
Define the following distance function 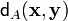 on the words
on the words 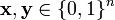 of length n transmitted via a Z-channel
of length n transmitted via a Z-channel
Define the sphere 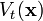 of radius t around a word
of radius t around a word 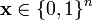 of length n as the set of all the words at distance t or less from
of length n as the set of all the words at distance t or less from 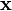 , in other words,
, in other words,
A code 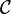 of length n is said to be t-asymmetric-error-correcting if for any two codewords
of length n is said to be t-asymmetric-error-correcting if for any two codewords 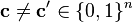 , one has
, one has 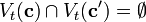 . Denote by
. Denote by 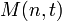 the maximum number of codewords in a t-asymmetric-error-correcting code of length n.
the maximum number of codewords in a t-asymmetric-error-correcting code of length n.
The Varshamov bound. For n≥1 and t≥1,
The constant-weight code bound. For n > 2t ≥ 2, let the sequence B0, B1, ..., Bn-2t-1 be defined as
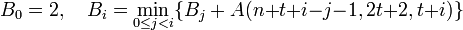 for
for 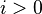 .
.
Then 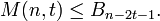
References
- T. Kløve, Error correcting codes for the asymmetric channel, Technical Report 18–09–07–81, Department of Informatics, University of Bergen, Norway, 1981.
- L.G. Tallini, S. Al-Bassam, B. Bose, On the capacity and codes for the Z-channel, Proceedings of the IEEE International Symposium on Information Theory, Lausanne, Switzerland, 2002, p. 422.