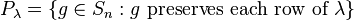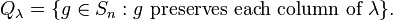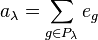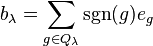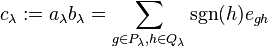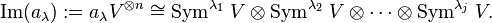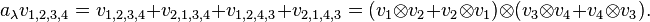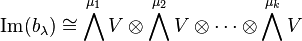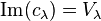Young symmetrizer

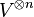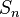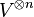In mathematics, a Young symmetrizer is an element of the group algebra of the symmetric group, constructed in such a way that, for the homomorphism from the group algebra to the endomorphisms of a vector space V^{\otimes n} obtained from the action of S_n on V^{\otimes n} by permutation of indices, the image of the endomorphism determined by that element corresponds to an irreducible representation of the symmetric group over the complex numbers. A similar construction works over any field, and the resulting representations are called Specht modules. The Young symmetrizer is named after British mathematician Alfred Young.

Definition

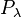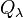Given a finite symmetric group Sn and specific Young tableau λ corresponding to a numbered partition of n, define two permutation subgroups P_\lambda and Q_\lambda of Sn as follows:

P_\lambda=\{ g\in S_n : g \text{ preserves each row of } \lambda \}

and

Q_\lambda=\{ g\in S_n : g \text{ preserves each column of } \lambda \}.

Corresponding to these two subgroups, define two vectors in the group algebra 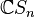\mathbb{C}S_n as

a_\lambda=\sum_{g\in P_\lambda} e_g

and

b_\lambda=\sum_{g\in Q_\lambda} \sgn(g) e_g

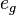where e_g is the unit vector corresponding to g, and 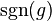\sgn(g) is the signature of the permutation. The product

c_\lambda := a_\lambda b_\lambda = \sum_{g\in P_\lambda,h\in Q_\lambda} \sgn(h) e_{gh}

is the Young symmetrizer corresponding to the Young tableau λ. Each Young symmetrizer corresponds to an irreducible representation of the symmetric group, and every irreducible representation can be obtained from a corresponding Young symmetrizer. (If we replace the complex numbers by more general fields the corresponding representations will not be irreducible in general.)

Construction

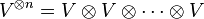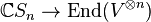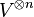Let V be any vector space over the complex numbers. Consider then the tensor product vector space V^{\otimes n}=V \otimes V \otimes \cdots \otimes V (n times). Let Sn act on this tensor product space by permuting the indices. One then has a natural group algebra representation \mathbb{C}S_n \rightarrow \text{End} (V^{\otimes n}) on V^{\otimes n}.

Given a partition λ of n, so that 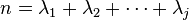n=\lambda_1+\lambda_2+ \cdots +\lambda_j, then the image of 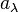a_\lambda is

\text{Im}(a_\lambda) := a_\lambda V^{\otimes n} \cong \text{Sym}^{\lambda_1}\; V \otimes \text{Sym}^{\lambda_2}\; V \otimes \cdots \otimes \text{Sym}^{\lambda_j}\; V.

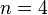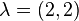For instance, if n =4, and \lambda = (2,2), with the canonical Young tableau 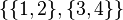\{\{1,2\},\{3,4\}\}. Then the corresponding 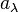a_\lambda is given by 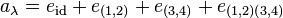a_\lambda = e_{\text{id}} + e_{(1,2)} + e_{(3,4)} + e_{(1,2)(3,4)}. Let an element in 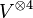V^{\otimes 4} be given by 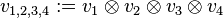v_{1,2,3,4}:=v_1 \otimes v_2 \otimes v_3 \otimes v_4. Then

a_\lambda v_{1,2,3,4} = v_{1,2,3,4} + v_{2,1,3,4} + v_{1,2,4,3} + v_{2,1,4,3} = (v_1 \otimes v_2 + v_2 \otimes v_1) \otimes (v_3 \otimes v_4 + v_4 \otimes v_3).

The latter clearly span 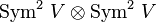\text{Sym}^2\; V\otimes \text{Sym}^2\; V.

The image of 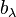b_\lambda is

\text{Im}(b_\lambda) \cong \bigwedge^{\mu_1} V \otimes \bigwedge^{\mu_2} V \otimes \cdots \otimes \bigwedge^{\mu_k} V

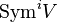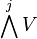where μ is the conjugate partition to λ. Here, \text{Sym}^i V and \bigwedge^j V are the symmetric and alternating tensor product spaces.

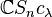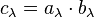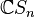The image \mathbb{C}S_nc_\lambda of c_\lambda = a_\lambda \cdot b_\lambda in \mathbb{C}S_n is an irreducible representation[1] of Sn, called a Specht module. We write

\text{Im}(c_\lambda) = V_\lambda

for the irreducible representation.

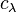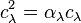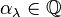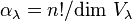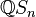Some scalar multiple of c_\lambda is idempotent, that is c^2_\lambda = \alpha_\lambda c_\lambda for some rational number \alpha_\lambda\in\mathbb{Q}. Specifically, one finds \alpha_\lambda=n! / \text{dim } V_\lambda. In particular, this implies that representations of the symmetric group can be defined over the rational numbers; that is, over the rational group algebra \mathbb{Q}S_n.

Consider, for example, S3 and the partition (2,1). Then one has 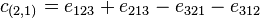c_{(2,1)} = e_{123}+e_{213}-e_{321}-e_{312}

If V is a complex vector space, then the images of 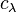c_\lambda on spaces 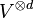V^{\otimes d} provides essentially all the finite-dimensional irreducible representations of GL(V).

See also

Notes

  1. ↑ See (Fulton & Harris 1991, Theorem 4.3, p. 46)

References