Youla–Kucera parametrization
In control theory the Youla–Kučera parametrization (also simply known as Youla parametrization) is a formula that describes all possible stabilizing feedback controllers for a given plant P, as function of a single parameter Q.
Details
The YK parametrization is a general result. It is a fundamental result of control theory and launched an entirely new area of research and found application, among others, in optimal and robust control.[1]
For ease of understanding and as suggested by Kučera it is best described for three increasingly general kinds of plant.
Stable SISO Plant
Let 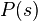 be a transfer function of a stable Single-input single-output system (SISO) system. Further, let Ω be a set of stable and proper functions of s. Then, the set of all proper stabilizing controllers for the plant
be a transfer function of a stable Single-input single-output system (SISO) system. Further, let Ω be a set of stable and proper functions of s. Then, the set of all proper stabilizing controllers for the plant 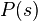 can be defined as
can be defined as
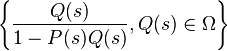 ,
,
where 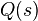 is an arbitrary proper and stable function of s. It can be said, that
is an arbitrary proper and stable function of s. It can be said, that 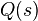 parametrizes all stabilizing controllers for the plant
parametrizes all stabilizing controllers for the plant 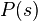 .
.
General SISO Plant
Consider a general plant with a transfer function 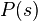 . Further, the transfer function can be factorized as
. Further, the transfer function can be factorized as
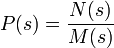 , where M(s), N(s) are stable and proper functions of s.
, where M(s), N(s) are stable and proper functions of s.
Now, solve the Bézout's identity of the form
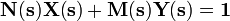 ,
,
where the variables to be found (X(s), Y(s)) must be also proper and stable.
After proper and stable X, Y were found, we can define one stabilizing controller that is of the form 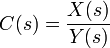 . After we have one stabilizing controller at hand, we can define all stabilizing controllers using a parameter Q(s) that is proper and stable. The set of all stabilizing controllers is defined as
. After we have one stabilizing controller at hand, we can define all stabilizing controllers using a parameter Q(s) that is proper and stable. The set of all stabilizing controllers is defined as
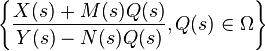 ,
,
General MIMO plant
In a multiple-input multiple-output (MIMO) system, consider a transfer matrix 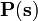 . It can be factorized using right coprime factors
. It can be factorized using right coprime factors 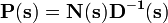 or left factors
or left factors 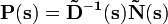 . The factors must be proper, stable and doubly coprime, which ensures that the system P(s) is controllable and observable. This can be written by Bézout identity of the form
. The factors must be proper, stable and doubly coprime, which ensures that the system P(s) is controllable and observable. This can be written by Bézout identity of the form
![\left[ \begin{matrix}
\mathbf{X} & \mathbf{Y} \\
-\mathbf{\tilde{N}} & {\mathbf{\tilde{D}}} \\
\end{matrix} \right]\left[ \begin{matrix}
\mathbf{D} & -\mathbf{\tilde{Y}} \\
\mathbf{N} & {\mathbf{\tilde{X}}} \\
\end{matrix} \right]=\left[ \begin{matrix}
\mathbf{I} & 0 \\
0 & \mathbf{I} \\
\end{matrix} \right]](../I/m/2587c7b46ff8b85882e589d9e366b66e.png) .
.
After finding 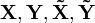 that are stable and proper, we can define the set of all stabilizing controllers K(s) using left or right factor, provided having negative feedback.
that are stable and proper, we can define the set of all stabilizing controllers K(s) using left or right factor, provided having negative feedback.
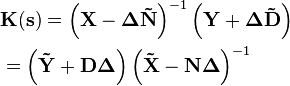
where 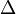 is an arbitrary stable and proper parameter.
is an arbitrary stable and proper parameter.
The engineering significance of the YK formula is that if one wants to find a stabilizing controller that meets some additional criterion, one can adjust Q such that the desired criterion is met.
References
- ↑ V. Kučera. A Method to Teach the Parameterization of All Stabilizing Controllers. 18th IFAC World Congress. Italy, Milan, 2011.
- D. C. Youla, H. A. Jabri, J. J. Bongiorno: Modern Wiener-Hopf design of optimal controllers: part II, IEEE Trans. Automat. Contr., AC-21 (1976) pp319–338
- V. Kučera: Stability of discrete linear feedback systems. In: Proceedings of the 6th IFAC. World Congress, Boston, MA, USA, (1975).
- C. A. Desoer, R.-W. Liu, J. Murray, R. Saeks. Feedback system design: the fractional representation approach to analysis and synthesis. IEEE Trans. Automat. Contr., AC-25 (3), (1980) pp399–412
- John Doyle, Bruce Francis, Allen Tannenbau. Feedback control theory. (1990).