Yao's test
In cryptography and the theory of computation, Yao's test is a test defined by Andrew Chi-Chih Yao in 1982 ,[1] against pseudo-random sequences. A sequence of words passes Yao's test if an attacker with reasonable computational power cannot distinguish it from a sequence generated uniformly at random.
Formal statement
Boolean circuits
Let  be a polynomial, and
be a polynomial, and 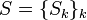 be a collection of sets
be a collection of sets 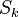 of
of 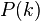 -bit long sequences, and for each
-bit long sequences, and for each  , let
, let 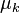 be a probability distribution on
be a probability distribution on 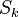 , and
, and 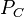 be a polynomial. A predicting collection
be a polynomial. A predicting collection 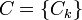 is a collection of boolean circuits of size less than
is a collection of boolean circuits of size less than 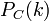 . Let
. Let 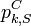 be the probability that on input
be the probability that on input  , a string randomly selected in
, a string randomly selected in 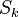 with probability
with probability 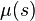 ,
, 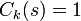 , i.e.
, i.e.
![p_{k,S}^C={\mathcal P}[C_k(s)=1 | s\in S_k\text{ with probability }\mu_k(s)]](../I/m/027b122afae3e9bbea620c95db23a654.png)
Moreover, let 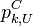 be the probability that
be the probability that 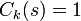 on input
on input  a
a 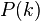 -bit long sequence selected uniformly at random in
-bit long sequence selected uniformly at random in 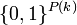 . We say that
. We say that  passes Yao's test if for all predicting collection
passes Yao's test if for all predicting collection  , for all but finitely many
, for all but finitely many  , for all polynomial
, for all polynomial 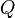 :
:
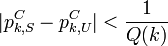
Probabilistic formulation
As in the case of the next-bit test, the predicting collection used in the above definition can be replaced by a probabilistic Turing machine, working in polynomial time. This also yields a strictly stronger definition of Yao's test (see Adleman's theorem). Indeed, One could decide undecidable properties of the pseudo-random sequence with the non-uniform circuits described above, whereas BPP machines can always be simulated by exponential-time deterministic Turing machines.
References
- ↑ Andrew Chi-Chih Yao. Theory and applications of trapdoor functions. In Proceedings of the 23rd IEEE Symposium on Foundations of Computer Science, 1982.