Y-homeomorphism
In mathematics, the y-homeomorphism, or crosscap slide, is a special type of auto-homeomorphism in non-orientable surfaces.
It can be constructed by sliding a Möbius band included on the surface
around an essential 1-sided closed curve until the original position; thus it is necessary that the surfaces have genus greater than one. The projective plane 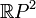 has no y-homeomorphism.
has no y-homeomorphism.
See also
- Lickorish-Wallace theorem
References
- J. S. Birman, D. R. J. Chillingworth, On the homeotopy group of a non-orientable surface, Trans. Amer. Math. Soc. 247 (1979), 87-124.
- D. R. J. Chillingworth, A finite set of generators for the homeotopy group of a non-orientable surface, Proc. Camb. Phil. Soc. 65 (1969), 409-430.
- M. Korkmaz, Mapping class group of non-orientable surface, Geometriae Dedicata 89 (2002), 109-133.
- W. B. R. Lickorish, Homeomorphisms of non-orientable two-manifolds, Math. Proc. Camb. Phil. Soc. 59 (1963), 307-317.