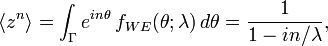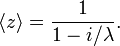Wrapped exponential distribution

Wrapped Exponential
Probability density function


The support is chosen to be [0,2π]

Cumulative distribution function


The support is chosen to be [0,2π]

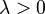Parameters \lambda>0
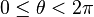Support 0\le\theta<2\pi
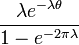PDF \frac{\lambda e^{-\lambda \theta}}{1-e^{-2\pi \lambda}}
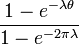CDF \frac{1-e^{-\lambda \theta}}{1-e^{-2\pi \lambda}}
Mean \arctan(1/\lambda) (circular)
Variance 1-\frac{\lambda}{\sqrt{1+\lambda^2}} (circular)
Entropy 1+\ln\left(\frac{\beta-1}{\lambda}\right)-\frac{\beta}{\beta-1}\ln(\beta) where \beta=e^{2\pi\lambda} (differential)
CF \frac{1}{1-in/\lambda}

In probability theory and directional statistics, a wrapped exponential distribution is a wrapped probability distribution that results from the "wrapping" of the exponential distribution around the unit circle.

Definition

The probability density function of the wrapped exponential distribution is[1]

f_{WE}(\theta;\lambda)=\sum_{k=0}^\infty \lambda e^{-\lambda (\theta+2 \pi k)}=\frac{\lambda e^{-\lambda \theta}}{1-e^{-2\pi \lambda}} ,

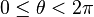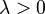for 0 \le \theta < 2\pi where \lambda > 0 is the rate parameter of the unwrapped distribution. This is identical to the truncated distribution obtained by restricting observed values X from the exponential distribution with rate parameter λ to the range 0\le X < 2\pi.

Characteristic function

The characteristic function of the wrapped exponential is just the characteristic function of the exponential function evaluated at integer arguments:

\varphi_n(\lambda)=\frac{1}{1-in/\lambda}

which yields an alternate expression for the wrapped exponential PDF:

f_{WE}(\theta;\lambda)=\frac{1}{2\pi}\sum_{n=-\infty}^\infty \frac{e^{in\theta}}{1-in/\lambda} .

Circular moments

In terms of the circular variable z=e^{i\theta} the circular moments of the wrapped exponential distribution are the characteristic function of the exponential distribution evaluated at integer arguments:

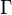\langle z^n\rangle=\int_\Gamma e^{in\theta}\,f_{WE}(\theta;\lambda)\,d\theta = \frac{1}{1-in/\lambda} ,

where \Gamma\, is some interval of length 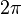2\pi. The first moment is then the average value of z, also known as the mean resultant, or mean resultant vector:

\langle z \rangle=\frac{1}{1-i/\lambda} .

The mean angle is

\langle \theta \rangle=\mathrm{Arg}\langle z \rangle = \arctan(1/\lambda) ,

and the length of the mean resultant is

R=|\langle z \rangle| = \frac{\lambda^2}{1+\lambda^2} .

Characterisation

The wrapped exponential distribution is the maximum entropy probability distribution for distributions restricted to the range 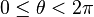0\le \theta < 2\pi for a fixed value of the expectation 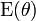\operatorname{E}(\theta).[1]

See also

References

  1. ↑ 1.0 1.1 Jammalamadaka, S. Rao; Kozubowski, Tomasz J. (2004). "New Families of Wrapped Distributions for Modeling Skew Circular Data". Communications in Statistics - Theory and Methods 33 (9): 2059–2074. doi:10.1081/STA-200026570. Retrieved 2011-06-13.