Wozencraft ensemble
In coding theory, the Wozencraft ensemble is a set of linear codes in which most of codes satisfy the Gilbert-Varshamov bound. It is named after John Wozencraft, who proved its existence. The ensemble is described by Massey (1963), who attributes it to Wozencraft. Justesen (1972) used the Wozencraft ensemble as the inner codes in his construction of strongly explicit asymptotically good code.
Existence theorem
Theorem: Let  > 0. For a large enough
> 0. For a large enough 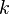 , there exists an ensemble of inner codes
, there exists an ensemble of inner codes 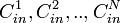 of rate
of rate  , where
, where 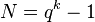 , such that for at least
, such that for at least 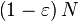 values of i,
values of i, 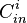 has relative distance
has relative distance 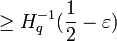 .
.
Here relative distance is the ratio of minimum distance to block length. And 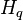 is the q-ary entropy function defined as follows:
is the q-ary entropy function defined as follows:
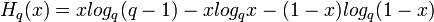 .
.
In fact, to show the existence of this set of linear codes, we will specify this ensemble explicitly as follows: for 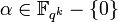 , the inner code
, the inner code 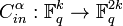 , is defined as
, is defined as 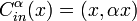 . Here we can notice that
. Here we can notice that 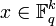 and
and 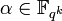 . We can do the multiplication
. We can do the multiplication 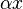 since
since 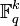 is isomorphic to
is isomorphic to 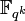 .
.
This ensemble is due to Wozencraft and is called the Wozencraft ensemble.
For any x and y in 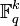 , we have the following facts:
, we have the following facts:
-
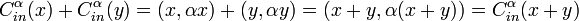
- For any
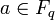 ,
, 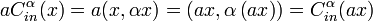
So 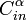 is a linear code for every
is a linear code for every 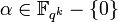 .
.
Now we know that Wozencraft ensemble contains linear codes with rate  . In the following proof, we will show that there are at least
. In the following proof, we will show that there are at least 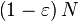 those linear codes having the relative distance
those linear codes having the relative distance 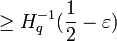 , i.e. they meet the Gilbert-Varshamov bound.
, i.e. they meet the Gilbert-Varshamov bound.
Proof
To prove that there are at least 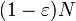 number of linear codes in the Wozencraft ensemble having relative distance
number of linear codes in the Wozencraft ensemble having relative distance 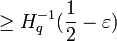 , we will prove that there are at most
, we will prove that there are at most 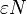 number of linear codes having relative distance <
number of linear codes having relative distance < 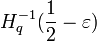 (i.e., having the distance <
(i.e., having the distance < 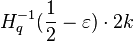 ).
).
Notice that in a linear code, the distance is equal to the minimum weight of all codewords of that code. This fact is the property of linear code. So if one non-zero codeword has the weight less than 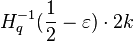 , then that code has the distance less than
, then that code has the distance less than 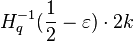 .
.
So  = the number of linear codes having the distance less than
= the number of linear codes having the distance less than 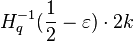 = the number of linear codes having some codeword that has the weight less than
= the number of linear codes having some codeword that has the weight less than 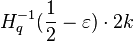 .
.
Now we have the following claim:
Claim: Two linear codes 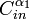 and
and 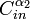 (here
(here 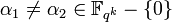 ) do not share any non-zero codeword.
) do not share any non-zero codeword.
Proof of Claim:
We prove the above claim by contradiction. Suppose there exist 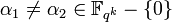 such that two linear codes
such that two linear codes 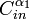 and
and 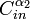 contain the same non-zero codeword y.
contain the same non-zero codeword y.
Now since 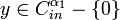 ,
, 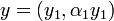 for some
for some 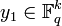 . As
. As 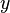 is non-zero,
is non-zero, 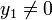 .
.
Similarly, 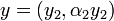 for some
for some 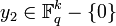 .
.
So 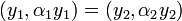 , then
, then 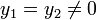 and
and 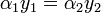 .
.
This implies 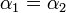 , which is a contradiction, which completes the proof of the claim.
, which is a contradiction, which completes the proof of the claim.
Now we come back to the proof of the theorem.
With any linear code having distance < 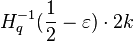 , it has some codeword that has the weight less than
, it has some codeword that has the weight less than 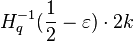 .
.
Also due to the Claim, notice that no two linear code share the same non-zero codewords. This implies that if we have  linear codes having distance <
linear codes having distance < 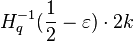 , then we have at least
, then we have at least  different
different 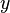 such that
such that 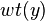 <
< 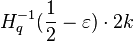 (one such codeword
(one such codeword 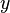 for each linear code). Here
for each linear code). Here 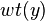 denotes the weight of codeword
denotes the weight of codeword 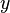 , which is the number of non-zero positions of
, which is the number of non-zero positions of 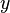 .
.
So  (the number of linear codes having distance <
(the number of linear codes having distance < 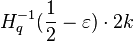 ) is less than or equal the number of non-zero
) is less than or equal the number of non-zero 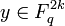 such that wt(y) <
such that wt(y) < 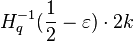 .
.
Denote 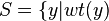 <
< 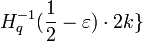
So 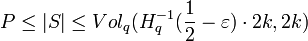
Here 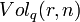 is the Volume of Hamming ball of radius r in
is the Volume of Hamming ball of radius r in ![[q]^n](../I/m/fd56f53f413fd36b409cfdc732be355d.png) .
.
Recall the upper bound of the Volume of Hamming ball 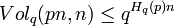 (check Bounds on the Volume of a Hamming ball for proof's detail), we have:
(check Bounds on the Volume of a Hamming ball for proof's detail), we have:
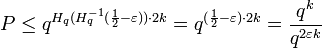
When 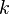 is large enough, we have
is large enough, we have 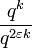 <
< 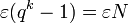
So  <
< 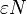 .
.
That means the number of linear codes having the relative distance < 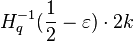 is less than
is less than 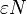 . So the number of linear codes having the relative distance at least
. So the number of linear codes having the relative distance at least 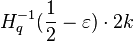 is greater than
is greater than 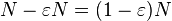 , which completes the proof.
, which completes the proof.
See also
References
- Massey, James L. (1963), Threshold decoding, Tech. Report 410, Cambridge, Mass.: Massachusetts Institute of Technology, Research Laboratory of Electronics, MR 0154763, hdl:1721.1/4415.
- Justesen, Jørn (1972), "A class of constructive asymptotically good algebraic codes", Institute of Electrical and Electronics Engineers. Transactions on Information Theory, IT-18: 652–656, doi:10.1109/TIT.1972.1054893, MR 0384313.
External links
- Lecture 28: Justesen Code. Coding theory's course. Prof. Atri Rudra.
- Lecture 9: Bounds on the Volume of a Hamming Ball. Coding theory's course. Prof. Atri Rudra.
- J. Justesen (1972). "A class of constructive asymptotically good algebraic codes". IEEE Trans. Info. Theory 18: 652–656. doi:10.1109/TIT.1972.1054893.
- Coding Theory's Notes: Gilbert-Varshamov Bound. Venkatesan Guruswami