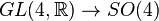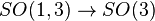World manifold
In gravitation theory, a world manifold endowed with some Lorentzian pseudo-Riemannian metric and an associated space-time structure is a space-time. Gravitation theory is formulated as classical field theory on natural bundles over a world manifold.
Topology
A world manifold is a four-dimensional orientable real smooth manifold. It is assumed to be a Hausdorff and second countable topological space. Consequently, it is a locally compact space which is a union of a countable number of compact subsets, a separable space, a paracompact and completely regular space. Being paracompact, a world manifold admits a partition of unity by smooth functions. It should be emphasized that paracompactness is an essential characteristic of a world manifold. It is necessary and sufficient in order that a world manifold admits a Riemannian metric and necessary for the existence of a pseudo-Riemannian metric. A world manifold is assumed to be connected and, consequently, it is arcwise connected.
Riemannian structure
The tangent bundle 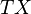 of a world manifold
of a world manifold  and the associated principal frame bundle
and the associated principal frame bundle 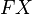 of linear tangent frames in
of linear tangent frames in 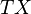 possess a general linear group structure group
possess a general linear group structure group 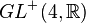 . A world manifold
. A world manifold  is said to be parallelizable if the tangent bundle
is said to be parallelizable if the tangent bundle 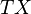 and, accordingly, the frame bundle
and, accordingly, the frame bundle 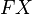 are trivial, i.e., there exists a global section (a frame field) of
are trivial, i.e., there exists a global section (a frame field) of 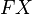 . It is essential that the tangent and associated bundles over a world manifold admit a bundle atlas of finite number of trivialization charts.
. It is essential that the tangent and associated bundles over a world manifold admit a bundle atlas of finite number of trivialization charts.
Tangent and frame bundles over a world manifold are natural bundles characterized by general covariant transformations. These transformations are gauge symmetries of gravitation theory on a world manifold.
By virtue of the well-known theorem on structure group reduction, a structure group 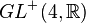 of a frame bundle
of a frame bundle 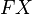 over a world manifold
over a world manifold  is always reducible to its maximal compact subgroup
is always reducible to its maximal compact subgroup 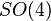 . The corresponding global section of the quotient bundle
. The corresponding global section of the quotient bundle 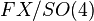 is a Riemannian metric
is a Riemannian metric 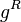 on
on  . Thus, a world manifold always admits a Riemannian metric which makes
. Thus, a world manifold always admits a Riemannian metric which makes  a metric topological space.
a metric topological space.
Lorentzian structure
In accordance with the geometric Equivalence Principle, a world manifold possesses a Lorentzian structure, i.e., a structure group of a frame bundle 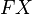 must be reduced to a Lorentz group
must be reduced to a Lorentz group 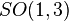 . The corresponding global section of the quotient bundle
. The corresponding global section of the quotient bundle 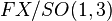 is a pseudo-Riemannian metric
is a pseudo-Riemannian metric  of signature
of signature 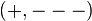 on
on  . It is treated as a gravitational field in General Relativity and as a classical Higgs field in gauge gravitation theory.
. It is treated as a gravitational field in General Relativity and as a classical Higgs field in gauge gravitation theory.
A Lorentzian structure need not exist. Therefore a world manifold is assumed to satisfy a certain topological condition. It is either a noncompact topological space or a compact space with a zero Euler characteristic. Usually, one also requires that a world manifold admits a spinor structure in order to describe Dirac fermion fields in gravitation theory. There is the additional topological obstruction to the existence of this structure. In particular, a noncompact world manifold must be parallelizable.
Space-time structure
If a structure group of a frame bundle 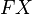 is reducible to a Lorentz group, the latter is always reducible to its maximal compact subgroup
is reducible to a Lorentz group, the latter is always reducible to its maximal compact subgroup 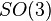 . Thus, there is the commutative diagram
. Thus, there is the commutative diagram
of the reduction of structure groups of a frame bundle 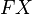 in
gravitation theory. This reduction diagram results in the following.
in
gravitation theory. This reduction diagram results in the following.
(i) In gravitation theory on a world manifold  , one can always choose an atlas of a frame bundle
, one can always choose an atlas of a frame bundle 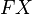 (characterized by local frame fields
(characterized by local frame fields 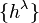 ) with
) with 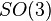 -valued transition functions. These transition functions preserve a time-like component
-valued transition functions. These transition functions preserve a time-like component 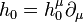 of local frame fields which, therefore, is globally defined. It is a nowhere vanishing vector field on
of local frame fields which, therefore, is globally defined. It is a nowhere vanishing vector field on  . Accordingly, the dual time-like covector field
. Accordingly, the dual time-like covector field 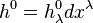 also is globally defined, and it yields a spatial distribution
also is globally defined, and it yields a spatial distribution
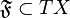 on
on  such that
such that 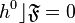 . Then the tangent bundle
. Then the tangent bundle 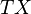 of a world manifold
of a world manifold  admits a space-time decomposition
admits a space-time decomposition
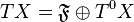 , where
, where 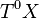 is a one-dimensional fibre bundle spanned by a time-like vector field
is a one-dimensional fibre bundle spanned by a time-like vector field 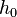 . This decomposition, is called the
. This decomposition, is called the  -compatible space-time structure. It makes a world manifold the space-time.
-compatible space-time structure. It makes a world manifold the space-time.
(ii) Given the above mentioned diagram of reduction of structure groups, let  and
and 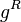 be the corresponding
pseudo-Riemannian and Riemannian metrics on
be the corresponding
pseudo-Riemannian and Riemannian metrics on  . They form a triple
. They form a triple 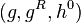 obeying the relation
obeying the relation
-
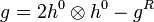 .
.
Conversely, let a world manifold  admit a nowhere vanishing
one-form
admit a nowhere vanishing
one-form  (or, equivalently, a nowhere vanishing vector
field). Then any Riemannian metric
(or, equivalently, a nowhere vanishing vector
field). Then any Riemannian metric 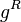 on
on  yields the
pseudo-Riemannian metric
yields the
pseudo-Riemannian metric
-
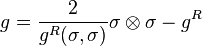 .
.
It follows that a world manifold  admits a pseudo-Riemannian
metric if and only if there exists a nowhere vanishing vector (or covector) field on
admits a pseudo-Riemannian
metric if and only if there exists a nowhere vanishing vector (or covector) field on  .
.
Let us note that a  -compatible Riemannian metric
-compatible Riemannian metric 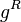 in a triple
in a triple 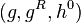 defines a
defines a  -compatible distance function on a world manifold
-compatible distance function on a world manifold  . Such a function brings
. Such a function brings  into a metric space whose locally Euclidean topology is equivalent to a manifold topology on
into a metric space whose locally Euclidean topology is equivalent to a manifold topology on  . Given a gravitational field
. Given a gravitational field  , the
, the  -compatible Riemannian metrics and the corresponding distance
functions are different for different spatial distributions
-compatible Riemannian metrics and the corresponding distance
functions are different for different spatial distributions 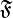 and
and 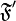 . It follows that physical observers associated with
these different spatial distributions perceive a world manifold
. It follows that physical observers associated with
these different spatial distributions perceive a world manifold  as different Riemannian spaces. The well-known relativistic changes of sizes of moving bodies exemplify this phenomenon.
as different Riemannian spaces. The well-known relativistic changes of sizes of moving bodies exemplify this phenomenon.
However, one attempts to derive a world topology directly from a space-time structure (a path topology, an Alexandrov topology). If a space-time satisfies the strong causality condition, such topologies coincide with a familiar manifold topology of a world manifold. In a general case, they however are rather extraordinary.
Causality conditions
A space-time structure is called integrable if a spatial distribution 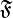 is involutive. In this case, its integral manifolds constitute a spatial foliation of a world manifold whose leaves are spatial three-dimensional subspaces. A spatial foliation is called causal if no curve transversal to its leaves intersects each leave more than once. This condition is equivalent to the stable causality of Stephen Hawking. A space-time foliation is causal if and only if it is a foliation of level surfaces of some smooth real function on
is involutive. In this case, its integral manifolds constitute a spatial foliation of a world manifold whose leaves are spatial three-dimensional subspaces. A spatial foliation is called causal if no curve transversal to its leaves intersects each leave more than once. This condition is equivalent to the stable causality of Stephen Hawking. A space-time foliation is causal if and only if it is a foliation of level surfaces of some smooth real function on  whose differential nowhere vanishes. Such a foliation is a fibred manifold
whose differential nowhere vanishes. Such a foliation is a fibred manifold 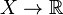 .
However, this is not the case of a compact world manifold which can not be
a fibred manifold over
.
However, this is not the case of a compact world manifold which can not be
a fibred manifold over 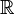 .
.
The stable causality does not provide the simplest causal structure. If a fibred manifold 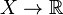 is a fibre bundle, it is trivial, i.e., a world manifold
is a fibre bundle, it is trivial, i.e., a world manifold  is a globally hyperbolic manifold
is a globally hyperbolic manifold 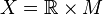 . Since any oriented three-dimensional manifold is parallelizable, a globally
hyperbolic world manifold is parallelizable.
. Since any oriented three-dimensional manifold is parallelizable, a globally
hyperbolic world manifold is parallelizable.
See also
References
- S.W. Hawking, G.F.R. Ellis, The Large Scale Structure of Space-Time (Cambridge Univ. Press, Cambridge, 1973) ISBN 0-521-20016-4
- C.T.G. Dodson, Categories, Bundles, and Spacetime Topology (Shiva Publ. Ltd., Orpington, UK, 1980) ISBN 0-906812-01-1
External links
- G. Sardanashvily, Classical gauge gravitation theory, Int. J. Geom. Methods Mod. Phys. 8 (2011) 1869; arXiv: 1110.1176