Wilks's lambda distribution

In statistics, Wilks's lambda distribution (named for Samuel S. Wilks), is a probability distribution used in multivariate hypothesis testing, especially with regard to the likelihood-ratio test and multivariate analysis of variance (MANOVA). It is a multivariate generalization of the univariate F-distribution, generalizing the F-distribution in the same way that the Hotelling's T-squared distribution generalizes Student's t-distribution.

Wilks's lambda distribution is related to two independent Wishart distributed variables, and is defined as follows,[1]

given

A \sim W_p(\Sigma, m) \qquad B \sim W_p(\Sigma, n)

independent and with 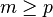m \ge p

\lambda = \frac{\det(A)}{\det(A+B)} = \frac{1}{\det(I+A^{-1}B)} \sim \Lambda(p,m,n)

where p is the number of dimensions. In the context of likelihood-ratio tests m is typically the error degrees of freedom, and n is the hypothesis degrees of freedom, so that 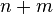n+m is the total degrees of freedom.[1]

The distribution can be related to a product of independent beta-distributed random variables

u_i \sim B\left(\frac{m+i-p}{2},\frac{p}{2}\right)
\prod_{i=1}^n u_i \sim \Lambda(p,m,n).

For large m, Bartlett's approximation[2] allows Wilks's lambda to be approximated with a chi-squared distribution

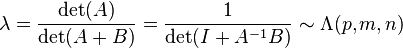
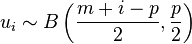
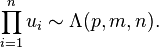
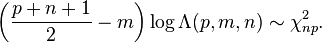
\left(\frac{p+n+1}{2}-m\right)\log \Lambda(p,m,n) \sim \chi^2_{np}.[1]

See also

References

  1. ↑ 1.0 1.1 1.2 Mardia, K. V.; Kent, J. T.; Bibby, J. M. (1979). Multivariate Analysis. Academic Press. ISBN 0-12-471250-9.
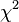  2. ↑ Bartlett, M.S. (1954). "A Note on the Multiplying Factors for Various \chi^2 Approximations". J R Stat Soc Series B 16 (2): 296–298. JSTOR 2984057.