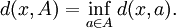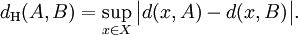Wijsman convergence
Wijsman convergence is a variation of Hausdorff convergence suitable for work with unbounded sets. Intuitively, Wijsman convergence is to convergence in the Hausdorff metric as pointwise convergence is to uniform convergence.
History
The convergence was defined by Robert Wijsman.[1] The same definition was used earlier by Zdeněk Frolík.[2] Yet earlier, Hausdorff in in his book Grundzüge der Mengenlehre defined so called closed limits; for proper metric spaces it is the same as Wijsman convergence.
Definition
Let (X, d) be a metric space and let Cl(X) denote the collection of all d-closed subsets of X. For a point x ∈ X and a set A ∈ Cl(X), set
A sequence (or net) of sets Ai ∈ Cl(X) is said to be Wijsman convergent to A ∈ Cl(X) if, for each x ∈ X,
Wijsman convergence induces a topology on Cl(X), known as the Wijsman topology.
Properties
- The Wijsman topology depends very strongly on the metric d. Even if two metrics are uniformly equivalent, they may generate different Wijsman topologies.
- Beer's theorem: if (X, d) is a complete, separable metric space, then Cl(X) with the Wijsman topology is a Polish space, i.e. it is separable and metrizable with a complete metric.
- Cl(X) with the Wijsman topology is always a Tychonoff space. Moreover, one has the Levi-Lechicki theorem: (X, d) is separable if and only if Cl(X) is either metrizable, first-countable or second-countable.
- If the pointwise convergence of Wijsman convergence is replaced by uniform convergence (uniformly in x), then one obtains Hausdorff convergence, where the Hausdorff metric is given by
- The Hausdorff and Wijsman topologies on Cl(X) coincide if and only if (X, d) is a totally bounded space.
References
- ↑ Wijsman, Robert A. (1966). "Convergence of sequences of convex sets, cones and functions. II". Trans. Amer. Math. Soc. (American Mathematical Society) 123 (1): 32–45. doi:10.2307/1994611. JSTOR 1994611. MR 0196599
- ↑ Z. Frolík, Concerning topological convergence of sets, Czechoskovak Math. J. 10 (1960), 168–180
- Beer, Gerald (1993). Topologies on closed and closed convex sets. Mathematics and its Applications 268. Dordrecht: Kluwer Academic Publishers Group. pp. xii+340. ISBN 0-7923-2531-1. MR 1269778
- Beer, Gerald (1994). "Wijsman convergence: a survey". Set-Valued Anal. 2 (1–2): 77–94. doi:10.1007/BF01027094. MR 1285822
External links
- Som Naimpally (2001), "Wijsman convergence", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4