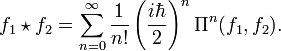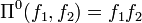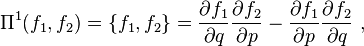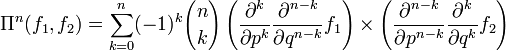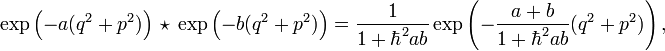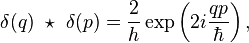Wigner–Weyl transform
In quantum mechanics, the Wigner–Weyl transform or Weyl–Wigner transform is the invertible mapping between functions in the quantum phase space formulation and Hilbert space operators in the Schrödinger picture. Often the mapping from phase space to operators is called the Weyl transform whereas the mapping from operators to phase space is called the Wigner transform. This mapping was originally devised by Hermann Weyl in 1927 in an attempt to map symmetrized classical phase space functions to operators, a procedure known as Weyl quantization or phase-space quantization.[1] It is now understood that Weyl quantization is not always well defined and sometimes gives unphysical answers.
Nevertheless, the mapping within quantum mechanics between the phase space and operator representations is well defined and is given by the Wigner–Weyl transform. Most importantly, the Wigner quasi-probability distribution is the Wigner transform of the quantum density matrix, and the density matrix is the Weyl transform of the Wigner function. In some contrast to Weyl's original intentions in seeking a consistent quantization scheme, this map merely amounts to a change of representation. It need not connect "classical" with "quantum" quantities: the starting phase-space function may well depend on Planck's constant ħ. Indeed, in some familiar cases involving angular momentum, it does. This invertible representation change then allows expressing quantum mechanics in phase space, as was appreciated in the 1940s by Groenewold[2] and Moyal.[3][4]
Example
The following illustrates the Weyl transformation on the simplest, two-dimensional Euclidean phase space. Let the coordinates on phase space be (q,p), and let f be a function defined everywhere on phase space.
The Weyl transform of the function f is given by the following operator in Hilbert space, broadly analogous to a Dirac delta function,
Here, the operators P and Q are taken to be the generators of a Lie algebra, the Heisenberg algebra:
where ħ is the reduced Planck constant. A general element of the Heisenberg algebra may thus be written as aQ+bP+c .
The exponential map of this element of the Lie algebra is then an element of the corresponding Lie group,
the Heisenberg group. Given a group representation ρ of the Heisenberg group on a Hilbert space, the operator
denotes the element of the representation corresponding to the group element g. By the Stone–von Neumann theorem, under suitable analytic hypotheses this representation is unique up to unitary equivalence, and the reader may imagine that it is the familiar one where P is the momentum operator and Q is the position operator. For this reason we will drop ρ in what follows.
This Weyl map may then also be expressed in terms of the integral kernel matrix elements of this operator,
The inverse of the above Weyl map is the Wigner map, which takes the operator Φ back to the original phase-space kernel function f,
In general, the resulting function f depends on Planck's constant ħ, and may well describe quantum-mechanical processes, provided it is properly composed through the star product, below.[5]
For example, the Wigner map of the quantum angular-momentum-squared operator L2 is not just the classical angular momentum squared, but it further contains an offset term − 3ħ2/2, which accounts for the nonvanishing angular momentum of the ground-state Bohr orbit.
Properties
Typically, the standard quantum-mechanical representation of the Heisenberg group is through its (Lie Algebra) generators: a pair of self-adjoint (Hermitian) operators on some Hilbert space  , such that their commutator, a central element of the algebra, amounts to the identity on that Hilbert space,
, such that their commutator, a central element of the algebra, amounts to the identity on that Hilbert space,
the quantum Canonical commutation relation. The Hilbert space may be taken to be the set of square integrable functions on the real number line (the plane waves). One may go beyond Hilbert spaces and work in a more general Schwartz space. Depending on the space involved, various results follow:
- If f is a real-valued function, then its Weyl-map image Φ[f] is self-adjoint.
- If f is an element of Schwartz space, then Φ[f] is trace-class.
- More generally, Φ[f] is a densely defined unbounded operator.
- For the standard representation of the Heisenberg group by square integrable functions, the map Φ[f] is one-to-one on the Schwartz space (as a subspace of the square-integrable functions).
Deformation quantization
Intuitively, a deformation of a mathematical object is a family of the same kind of objects that depend on some parameter(s). Here, it provides rules for how to deform the "classical" commutative algebra of observables to a quantum non-commutative algebra of observables.
The basic setup in deformation theory is to start with an algebraic structure (say a Lie algebra) and ask: Does there exist a one or more parameter(s) family of similar structures, such that for an initial value of the parameter(s) one has the same structure (Lie algebra) one started with? (The oldest illustration of this may be the realization of Eratosthenes in the ancient world that a flat earth was deformable to a spherical earth, with deformation parameter 1/R⊕.) E.g., one may define a noncommutative torus as a deformation quantization through a ★-product to implicitly address all convergence subtleties (usually not addressed in formal deformation quantization). Insofar as the algebra of functions on a space determines the geometry of that space, the study of the star product leads to the study of a non-commutative geometry deformation of that space.
In the context of the above flat phase-space example, the star product (Moyal product, actually introduced by Groenewold in 1946), ★ħ, of a pair of functions in f1, f2 ∈ C∞(ℜ2), is specified by
The star product is not commutative in general, but goes over to the ordinary commutative product of functions in the limit of ħ → 0. As such, it is said to define a deformation of the commutative algebra of C∞(ℜ2).
For the Weyl-map example above, the ★-product may be written in terms of the Poisson bracket as
Here, Π is the Poisson bivector, an operator defined such that its powers are
and
where {f1, f2} is the Poisson bracket. More generally,
where  is the binomial coefficient.
is the binomial coefficient.
Thus, e.g.,[6] Gaussians compose hyperbolically,
or
etc. These formulas are predicated on coordinates in which the Poisson bivector is constant (plain flat Poisson brackets). For the general formula on arbitrary Poisson manifolds, cf. the Kontsevich quantization formula.
Antisymmetrization of this ★-product yields the Moyal bracket, the proper quantum deformation of the Poisson bracket, and the phase-space isomorph (Wigner transform) of the quantum commutator in the more usual Hilbert-space formulation of quantum mechanics. As such, it provides the cornerstone of the dynamical equations of observables in this phase-space formulation.
There results a complete phase space formulation of quantum mechanics, completely equivalent to the Hilbert-space operator representation, with star-multiplications paralleling operator multiplications isomorphically.[6]
Expectation values in phase-space quantization are obtained isomorphically to tracing operator observables Φ with the density matrix in Hilbert space: they are obtained by phase-space integrals of observables such as the above f with the Wigner quasi-probability distribution effectively serving as a measure.
Thus, by expressing quantum mechanics in phase space (the same ambit as for classical mechanics), the above Weyl map facilitates recognition of quantum mechanics as a deformation (generalization, cf. correspondence principle) of classical mechanics, with deformation parameter ħ/S. (Other familiar deformations in physics involve the deformation of classical Newtonian into relativistic mechanics, with deformation parameter v/c; or the deformation of Newtonian gravity into General Relativity, with deformation parameter Schwarzschild-radius/characteristic-dimension. Conversely, group contraction leads to the vanishing-parameter undeformed theories—classical limits.)
Classical expressions, observables, and operations (such as Poisson brackets) are modified by ħ-dependent quantum corrections, as the conventional commutative multiplication applying in classical mechanics is generalized to the noncommutative star-multiplication characterizing quantum mechanics and underlying its uncertainty principle.
Generalizations
In more generality, Weyl quantization is studied in cases where the phase space is a symplectic manifold, or possibly a Poisson manifold. Related structures include the Poisson–Lie groups and Kac–Moody algebras.
See also
|
References
- ↑ Weyl, H. (1927). "Quantenmechanik und Gruppentheorie". Zeitschrift für Physik 46: 1–46. Bibcode:1927ZPhy...46....1W. doi:10.1007/BF02055756.
- ↑ Groenewold, H. J. (1946). "On the Principles of elementary quantum mechanics". Physica 12 (7): 405–446. Bibcode:1946Phy....12..405G. doi:10.1016/S0031-8914(46)80059-4.
- ↑ Moyal, J. E.; Bartlett, M. S. (1949). "Quantum mechanics as a statistical theory". Mathematical Proceedings of the Cambridge Philosophical Society 45: 99. doi:10.1017/S0305004100000487.
- ↑ Curtright, T. L.; Zachos, C. K. (2012). "Quantum Mechanics in Phase Space". Asia Pacific Physics Newsletter 1: 37. arXiv:1104.5269. doi:10.1142/S2251158X12000069.
- ↑ Kubo, R. (1964). "Wigner Representation of Quantum Operators and Its Applications to Electrons in a Magnetic Field". Journal of the Physical Society of Japan 19 (11): 2127–2139. doi:10.1143/JPSJ.19.2127.
- ↑ 6.0 6.1 Zachos, C. K.; Fairlie, D. B.; Curtright, T. L. (2005). Quantum Mechanics in Phase Space. World Scientific. ISBN 978-981-238-384-6.
Further reading
- Case, William B. (October 2008). "Wigner functions and Weyl transforms for pedestrians". American Journal of Physics 76 (10): 937–946. Bibcode:2008AmJPh..76..937C. doi:10.1119/1.2957889. (Sections I to IV of this article provide an overview over the Wigner–Weyl transform, the Wigner quasiprobability distribution, the phase space formulation of quantum mechanics and the example of the quantum harmonic oscillator.)
- Hazewinkel, Michiel, ed. (2001), "Weyl quantization", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
![\Phi_\rho [f] = \frac{1}{(2\pi)^2}\iint\!\!\! \iint f(q,p) \rho\left(e^{i(a(Q-q)
+b(P-p))}\right) \text{d}q\, \text{d}p\, \text{d}a\, \text{d}b.](../I/m/ea3b19d1f497c12d8c66d278c4d0029d.png)
![[P,Q]=PQ-QP=-i\hbar,\,](../I/m/322b63327aaf53a619357a623709e8b5.png)
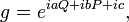
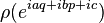
![\langle x| \Phi [f] |y \rangle = \int_{-\infty}^\infty {\text{d}p\over h} ~e^{ip(x-y)/\hbar}~ f\left({x+y\over2},p\right) .](../I/m/21846cbc41b2c325a0399189196d5fff.png)
![f(q,p)= 2 \int_{-\infty}^\infty \text{d}y~e^{-2ipy/\hbar}~ \langle q+y| \Phi [f] |q-y \rangle.](../I/m/b950f4fae81c205f1e895974a98ab069.png)
![[P,Q]=PQ-QP=-i\hbar ~ \operatorname{Id}_\mathcal{H},](../I/m/66d3b90cad1cbb4c152be13e76eb31ad.png)
![\Phi [f_1 \star f_2] = \Phi [f_1]\Phi [f_2].\,](../I/m/a5ed32bccce72d83af5d4cc7c191c989.png)