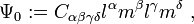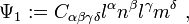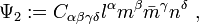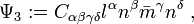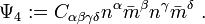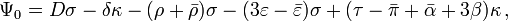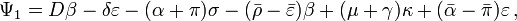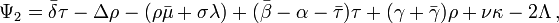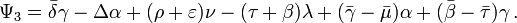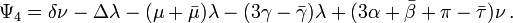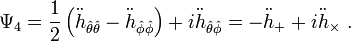Weyl scalar
In the Newman–Penrose (NP) formalism of general relativity, Weyl scalars refer to a set of five complex scalars 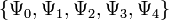 which encode the ten independent components of the Weyl tensors of a four-dimensional spacetime.
which encode the ten independent components of the Weyl tensors of a four-dimensional spacetime.
Definitions
Given a complex null tetrad 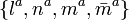 and with the convention
and with the convention 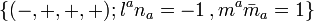 , the Weyl-NP scalars are defined by[1][2][3]
, the Weyl-NP scalars are defined by[1][2][3]
Note: If one adopts the convention 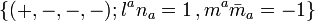 , the definitions of
, the definitions of 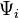 should take the opposite values;[4][5][6][7] that is to say,
should take the opposite values;[4][5][6][7] that is to say, 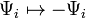 after the signature transition.
after the signature transition.
Alternative derivations
According to the definitions above, one should find out the Weyl tensors before calculating the Weyl-NP scalars via contractions with relevant tetrad vectors. This method, however, does not fully reflect the spirit of Newman–Penrose formalism. As an alternative, one could firstly compute the spin coefficients and then derive the five Weyl-NP scalars via the following NP field equations,
where 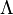 (used for
(used for 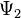 ) refers to the NP curvature scalar
) refers to the NP curvature scalar 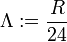 which could be calculated directly from the spacetime metric
which could be calculated directly from the spacetime metric 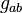 .
.
Physical interpretation
Szekeres (1965)[8] gave an interpretation of the different Weyl scalars at large distances:
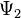 is a "Coulomb" term, representing the gravitational monopole of the source;
is a "Coulomb" term, representing the gravitational monopole of the source;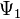 &
& 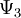 are ingoing and outgoing "longitudinal" radiation terms;
are ingoing and outgoing "longitudinal" radiation terms;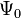 &
& 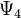 are ingoing and outgoing "transverse" radiation terms.
are ingoing and outgoing "transverse" radiation terms.
For a general asymptotically flat spacetime containing radiation (Petrov Type I), 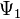 &
& 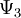 can be transformed to zero by an appropriate choice of null tetrad. Thus these can be viewed as gauge quantities.
can be transformed to zero by an appropriate choice of null tetrad. Thus these can be viewed as gauge quantities.
A particularly important case is the Weyl scalar 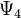 .
It can be shown to describe outgoing gravitational radiation (in an asymptotically flat spacetime) as
.
It can be shown to describe outgoing gravitational radiation (in an asymptotically flat spacetime) as
Here, 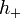 and
and 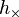 are the "plus" and "cross" polarizations of gravitational radiation, and the double dots represent double time-differentiation.
are the "plus" and "cross" polarizations of gravitational radiation, and the double dots represent double time-differentiation.
There are, however, certain examples in which the interpretation listed above fails.[9] These are exact vacuum solutions of the Einstein field equations with cylindrical symmetry. For instance, a static (infinitely long) cylinder can produce a gravitational field which has not only the expected "Coulomb"-like Weyl component 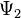 , but also non-vanishing "transverse wave"-components
, but also non-vanishing "transverse wave"-components 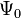 and
and 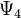 . Furthermore, purely outgoing Einstein-Rosen waves have a non-zero "incoming transverse wave"-component
. Furthermore, purely outgoing Einstein-Rosen waves have a non-zero "incoming transverse wave"-component 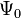 .
.
See also
References
- ↑ Jeremy Bransom Griffiths, Jiri Podolsky. Exact Space-Times in Einstein's General Relativity. Cambridge: Cambridge University Press, 2009. Chapter 2.
- ↑ Valeri P Frolov, Igor D Novikov. Black Hole Physics: Basic Concepts and New Developments. Berlin: Springer, 1998. Appendix E.
- ↑ Abhay Ashtekar, Stephen Fairhurst, Badri Krishnan. Isolated horizons: Hamiltonian evolution and the first law. Physical Review D, 2000, 62(10): 104025. Appendix B. gr-qc/0005083
- ↑ Ezra T Newman, Roger Penrose. An Approach to Gravitational Radiation by a Method of Spin Coefficients. Journal of Mathematical Physics, 1962, 3(3): 566-768.
- ↑ Ezra T Newman, Roger Penrose. Errata: An Approach to Gravitational Radiation by a Method of Spin Coefficients. Journal of Mathematical Physics, 1963, 4(7): 998.
- ↑ Subrahmanyan Chandrasekhar. The Mathematical Theory of Black Holes. Chicago: University of Chikago Press, 1983.
- ↑ Peter O'Donnell. Introduction to 2-Spinors in General Relativity. Singapore: World Scientific, 2003.
- ↑ P. Szekeres (1965). "The Gravitational Compass". Journal of Mathematical Physics 6 (9): 1387–1391. Bibcode:1965JMP.....6.1387S. doi:10.1063/1.1704788..
- ↑ Hofmann, Stefan; Niedermann, Florian; Schneider, Robert (2013). "Interpretation of the Weyl tensor". Phys.Rev. D88: 064047. doi:10.1103/PhysRevD.88.064047.