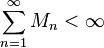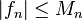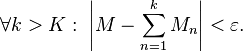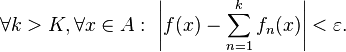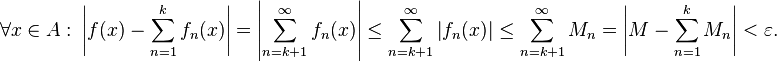Weierstrass M-test

In mathematics, the Weierstrass M-test is a test for showing that an infinite series of functions converges uniformly. It applies to series whose terms are functions with real or complex values, and is analogous to the comparison test for determining the convergence of series of real or complex numbers.

The Weierstrass M-test is a special case of Lebesgue's dominated convergence theorem, where the measure is taken to be the counting measure over an atomic measure space.

Statement

Weierstrass M-test. Suppose that {f_n} is a sequence of real- or complex-valued functions defined on a set A, and that there is a sequence of positive numbers {M_n} satisfying
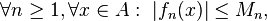
$\forall n \geq 1, \forall x \in A: \ |f_n(x)|\leq M_n,$

$\sum_{n=1}^{\infty} M_n < \infty$

Then the series

$\sum_{n=1}^{\infty} f_n (x)$
converges uniformly on A.

Remark. The result is often used in combination with the uniform limit theorem. Together they say that if, in addition to the above conditions, the set A is a topological space and the functions f_n are continuous on A, then the series converges to a continuous function.

Generalization

A more general version of the Weierstrass M-test holds if the codomain of the functions {f_n} is any Banach space, in which case the statement

|f_n|\leq M_n

may be replaced by

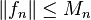\|f_n\|\leq M_n

where $\|\cdot\|$ is the norm on the Banach space. For an example of the use of this test on a Banach space, see the article Fréchet derivative.

Proof

Let M be the limit of the sum 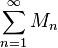$\sum_{n=1}^{\infty} M_n$ . Since 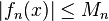$|f_n(x)| \le M_n$ the sum 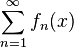$\sum_{n=1}^{\infty} f_n(x)$ is absolutely convergent, call its limit f(x).

By convergence of the M sum, for ε > 0 there exists an integer K such that

\forall k > K: \ \left|M - \sum_{n=1}^{k} M_n\right| < \varepsilon.

We will show that 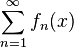$\sum_{n=1}^{\infty} f_n(x)$ converges uniformly on the set A by showing that

\forall k > K, \forall x \in A: \ \left|f(x) - \sum_{n=1}^{k} f_n(x)\right| < \varepsilon.

The crucial point here is that K does not depend on x.

\forall x \in A: \ \left|f(x) - \sum_{n=1}^{k} f_n(x)\right| = \left|\sum_{n=k+1}^{\infty} f_n(x)\right| \le \sum_{n=k+1}^{\infty} \left|f_n(x)\right| \le \sum_{n=k+1}^{\infty} M_n = \left|M - \sum_{n=1}^{k} M_n\right| < \varepsilon.

References

Rudin, Walter (January 1991). Functional Analysis. McGraw-Hill Science/Engineering/Math. ISBN 0-07-054236-8.
Rudin, Walter (May 1986). Real and Complex Analysis. McGraw-Hill Science/Engineering/Math. ISBN 0-07-054234-1.
Rudin, Walter (1976). Principles of Mathematical Analysis. McGraw-Hill Science/Engineering/Math.
Whittaker; Watson (1927). A Course in Modern Analysis (Fourth ed.). Cambridge University Press. p. 49.

Weierstrass M-test

Statement

Generalization

Proof

See also

References