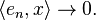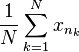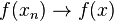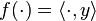Weak convergence (Hilbert space)
In mathematics, weak convergence in a Hilbert space is convergence of a sequence of points in the weak topology.
Properties
- If a sequence converges strongly, then it converges weakly as well.
- Since every closed and bounded set is weakly relatively compact (its closure in the weak topology is compact), every bounded sequence
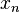 in a Hilbert space H contains a weakly convergent subsequence. Note that closed and bounded sets are not in general weakly compact in Hilbert spaces (consider the set consisting of an orthonormal basis in an infinitely dimensional Hilbert space which is closed and bounded but not weakly compact since it doesn't contain 0). However, bounded and weakly closed sets are weakly compact so as a consequence every convex bounded closed set is weakly compact.
in a Hilbert space H contains a weakly convergent subsequence. Note that closed and bounded sets are not in general weakly compact in Hilbert spaces (consider the set consisting of an orthonormal basis in an infinitely dimensional Hilbert space which is closed and bounded but not weakly compact since it doesn't contain 0). However, bounded and weakly closed sets are weakly compact so as a consequence every convex bounded closed set is weakly compact.
- As a consequence of the principle of uniform boundedness, every weakly convergent sequence is bounded.
- The norm is (sequentially) weakly lower-semicontinuous: if
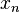 converges weakly to x, then
converges weakly to x, then
- and this inequality is strict whenever the convergence is not strong. For example, infinite orthonormal sequences converge weakly to zero, as demonstrated below.
- If
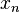 converges weakly to
converges weakly to  and we have the additional assumption that
and we have the additional assumption that 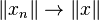 , then
, then 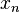 converges to
converges to  strongly:
strongly:
- If the Hilbert space is finite-dimensional, i.e. a Euclidean space, then the concepts of weak convergence and strong convergence are the same.
Example
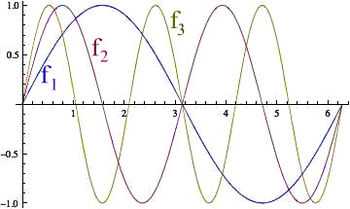
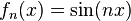 on
on ![[0, 2 \pi]](../I/m/58c9a5de0cb1a343ae0acd1fb191eea1.png) . As
. As 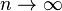
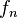 converges weakly to
converges weakly to 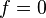 .
.The Hilbert space ![L^2[0, 2\pi]](../I/m/06c5f590661ae01584af1396e66020ad.png) is the space of the square-integrable functions on the interval
is the space of the square-integrable functions on the interval ![[0, 2\pi]](../I/m/58c9a5de0cb1a343ae0acd1fb191eea1.png) equipped with the inner product defined by
equipped with the inner product defined by
(see Lp space). The sequence of functions  defined by
defined by
converges weakly to the zero function in ![L^2[0, 2\pi]](../I/m/06c5f590661ae01584af1396e66020ad.png) , as the integral
, as the integral
tends to zero for any square-integrable function  on
on ![[0, 2\pi]](../I/m/58c9a5de0cb1a343ae0acd1fb191eea1.png) when
when  goes to infinity, i.e.
goes to infinity, i.e.
Although 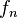 has an increasing number of 0's in
has an increasing number of 0's in ![[0,2 \pi]](../I/m/58c9a5de0cb1a343ae0acd1fb191eea1.png) as
as  goes to infinity, it is of course not equal to the zero function for any
goes to infinity, it is of course not equal to the zero function for any  . Note that
. Note that 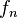 does not converge to 0 in the
does not converge to 0 in the 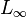 or
or 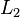 norms. This dissimilarity is one of the reasons why this type of convergence is considered to be "weak."
norms. This dissimilarity is one of the reasons why this type of convergence is considered to be "weak."
Weak convergence of orthonormal sequences
Consider a sequence 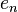 which was constructed to be orthonormal, that is,
which was constructed to be orthonormal, that is,
where 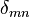 equals one if m = n and zero otherwise. We claim that if the sequence is infinite, then it converges weakly to zero. A simple proof is as follows. For x ∈ H, we have
equals one if m = n and zero otherwise. We claim that if the sequence is infinite, then it converges weakly to zero. A simple proof is as follows. For x ∈ H, we have
where equality holds when {en} is a Hilbert space basis. Therefore
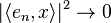 (since the series above converges, its corresponding sequence must go to zero)
(since the series above converges, its corresponding sequence must go to zero)
i.e.
Banach–Saks theorem
The Banach–Saks theorem states that every bounded sequence 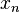 contains a subsequence
contains a subsequence  and a point x such that
and a point x such that
converges strongly to x as N goes to infinity.
Generalizations
The definition of weak convergence can be extended to Banach spaces. A sequence of points 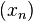 in a Banach space B is said to converge weakly to a point x in B if
in a Banach space B is said to converge weakly to a point x in B if
for any bounded linear functional  defined on
defined on  , that is, for any
, that is, for any  in the dual space
in the dual space 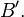 If
If  is a Hilbert space, then, by the Riesz representation theorem, any such
is a Hilbert space, then, by the Riesz representation theorem, any such  has the form
has the form
for some  in
in  , so one obtains the Hilbert space definition of weak convergence.
, so one obtains the Hilbert space definition of weak convergence.
| ||||||||||||||||||||||||||||||||||
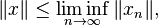
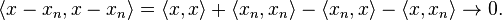
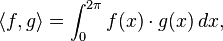
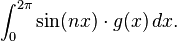
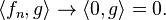
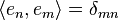
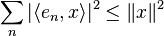 (
(