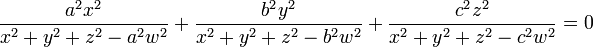Wave surface

In mathematics, Fresnel's wave surface, found by Augustin-Jean Fresnel in 1821, is a quartic surface describing the propagation of light in an optically biaxial crystal. Wave surfaces are special cases of tetrahedroids which are in turn special cases of Kummer surfaces.

In projective coordinates (w:x:y:z) the wave surface is given by

\frac{a^2x^2}{x^2+y^2+z^2-a^2w^2} + \frac{b^2y^2}{x^2+y^2+z^2-b^2w^2} + \frac{c^2z^2}{x^2+y^2+z^2-c^2w^2} =0

References

Bateman, H. (1910), "Kummer's quartic surface as a wave surface.", Proceedings of the London Mathematical Society 8 (1): 375–382, doi:10.1112/plms/s2-8.1.375, ISSN 0024-6115
Cayley, Arthur (1846), "Sur la surface des ondes", Journal des Mathématiques Pures et Appliquées 11: 291–296, Collected papers vol 1 pages 302–305
Knörrer, H. (1986), "Die Fresnelsche Wellenfläche", Arithmetik und Geometrie, Math. Miniaturen 3, Basel, Boston, Berlin: Birkhäuser, pp. 115–141, ISBN 978-3-7643-1759-1, MR 879281
Love, A. E. H. (2011) [1927], A treatise on the Mathematical Theory of Elasticity, Dover Publications, New York, ISBN 978-0-486-60174-8, MR 0010851

External links

Fresnel wave surface