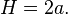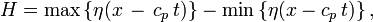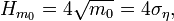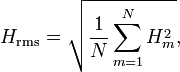Wave height

Merchant ship labouring in heavy seas as a huge wave looms astern

In fluid dynamics, the wave height of a surface wave is the difference between the elevations of a crest and a neighbouring trough.[1] Wave height is a term used by mariners, as well as in coastal, ocean and naval engineering.

At sea, the term significant wave height is used as a means to introduce a well-defined and standardized statistic to denote the characteristic height of the random waves in a sea state. It is defined in such a way that it more–or–less corresponds to what a mariner observes when estimating visually the average wave height.

Several definitions for different situations

Wave characteristics.
H = 2a. \,
H = \max\left\{ \eta(x\,-\,c_p\,t) \right\} - \min\left\{ \eta(x - c_p\,t) \right\}, \,
with cp the phase speed (or propagation speed) of the wave. The sine wave is a specific case of a periodic wave.
H_{1/3} = \frac{1}{\frac13\,N}\, \sum_{m=1}^{\frac13\,N}\, H_m,
with Hm the individual wave heights, sorted in such a way that the highest wave has m=1 and the lowest wave is for m=N. Only the highest one-third is used, since this corresponds best with visual observations of experienced mariners: eyes and brain apparently focus on the higher waves seen.[2]
H_{m_0} = 4 \sqrt{m_0} = 4 \sigma_\eta, \,
where m0, the zeroth-moment of the variance spectrum, is obtained by integration of the variance spectrum. In case of a measurement, the standard deviation ση is the easiest and most accurate statistic to be used.
H_\text{rms} = \sqrt{ \frac{1}{N} \sum_{m=1}^N H_m^2}, \,
with Hm again denoting the individual wave heights in a certain time series.

See also

Notes

  1. ↑ 1.0 1.1 1.2 Kinsman (1984, p. 38)
  2. ↑ 2.0 2.1 2.2 2.3 Holthuijsen (2007, pp. 24–28)
  3. ↑ Holthuijsen (2007, p. 70)

References

  • Holthuijsen, Leo H. (2007), Waves in Oceanic and Coastal Waters, Cambridge University Press, ISBN 0-521-86028-8, 387 pages.
  • Kinsman, Blair (1984), Wind waves: their generation and propagation on the ocean surface, Dover Publications, ISBN 0-486-49511-6, 704 pages.
  • Phillips, Owen M. (1977), The dynamics of the upper ocean (2nd ed.), Cambridge University Press, ISBN 0-521-29801-6, viii & 336 pages.