Wave function renormalization
In quantum field theory, wave function renormalization is a rescaling, or renormalization, of quantum fields to take into account the effects of interactions. For a noninteracting or free field, the field operator creates or annihilates a single particle with probability 1. Once interactions are included, however, this probability is modified in general to Z 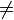 1. This shows up when one calculates the propagator beyond leading order; e.g., for a scalar field,
1. This shows up when one calculates the propagator beyond leading order; e.g., for a scalar field,
(The shift of the mass from m0 to m constitutes the mass renormalization.)
One possible wave function renormalization, which happens to be scale independent, is to rescale the fields so that the Lehmann weight (Z in the formula above) of their quanta is 1. (It's trickier to define it for unstable particles). For the purposes of studying renormalization group flows, if the coefficient of the kinetic term in the action at the scale Λ is Z, then the field is rescaled by  . A scale dependent wavefunction renormalization for a field means that that field has an anomalous scaling dimension.
. A scale dependent wavefunction renormalization for a field means that that field has an anomalous scaling dimension.