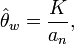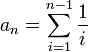Watterson estimator

In population genetics, the Watterson estimator is a method for estimating the population mutation rate, 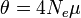$\theta = 4N_e\mu$ , where 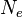$N_e$ is the effective population size and $\mu$ is the per-generation mutation rate of the population of interest (Watterson (1975)). 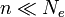The assumptions made are that there is a sample of n haploid individuals from the population of interest, that there are infinitely many sites capable of varying (so that mutations never overlay or reverse one another), and that $n \ll N_e$ .

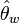The estimate of $\theta$ , often denoted as ${\hat \theta_w}$ , is

{\hat \theta_w} = { K \over a_n },

where K is the number of segregating sites (an example of a segregating site would be a single-nucleotide polymorphism) in the sample and

a_n = \sum^{n-1}_{i=1} {1 \over i}

is the (n − 1)th harmonic number.

This estimate is based on coalescent theory. Watterson's estimator is commonly used for its simplicity. When its assumptions are met, the estimator is unbiased and the variance of the estimator decreases with increasing sample size or recombination rate. However, the estimator can be biased by population structure. For example, 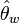${\hat\theta_w}$ is downwardly biased in an exponentially growing population. It can also be biased by violation of the infinite-sites mutational model; if multiple mutations can overwrite one another, Watterson's estimator will be biased downward.

References

Watterson, G.A. (1975), "On the number of segregating sites in genetical models without recombination.", Theoretical Population Biology 7 (2): 256–276, doi:10.1016/0040-5809(75)90020-9, PMID 1145509
McVean, Gil; Awadalla, Philip; Fearnhead, Paul (2002) "A Coalescent-Based Method for Detecting and Estimating Recombination From Gene Sequences", Genetics, 160, 1231–1241.

Watterson estimator

See also

References