Wald's equation
In probability theory, Wald's equation, Wald's identity[1] or Wald's lemma[2] is an important identity that simplifies the calculation of the expected value of the sum of a random number of random quantities. In its simplest form, it relates the expectation of a sum of randomly many finite-mean, independent and identically distributed random variables to the expected number of terms in the sum and the random variables' common expectation under the condition that the number of terms in the sum is independent of the summands.
The equation is named after the mathematician Abraham Wald. An identity for the second moment is given by the Blackwell–Girshick equation.
Basic version
Let (Xn)n∈ℕ be a sequence of real-valued, independent and identically distributed random variables and let N be a nonnegative integer-value random variable that is independent of the sequence (Xn)n∈ℕ. Suppose that N and the Xn have finite expectations. Then
Example
Roll a six-sided die. Take the number on the die (call it N) and roll that number of six-sided dice to get the numbers X1, . . . , XN, and add up their values. By Wald's equation, the resulting value on average is
General version
Let (Xn)n∈ℕ be an infinite sequence of real-valued random variables and let N be a nonnegative integer-valued random variable. Assume that
- 1. (Xn)n∈ℕ are all integrable (finite-mean) random variables,
- 2. E[Xn1{N ≥ n}] = E[Xn] P(N ≥ n) for every natural number n, and
- 3. the infinite series satisfies
Then the random sums
are integrable and
If, in addition,
- 4. (Xn)n∈ℕ all have the same expectation, and
- 5. N has finite expectation,
then
Remark: Usually, the name Wald's equation refers to this last equality.
Discussion of assumptions
Clearly, assumption (1) is needed to formulate assumption (2) and Wald's equation. Assumption (2) controls the amount of dependence allowed between the sequence (Xn)n∈ℕ and the number N of terms; see the counterexample below for the necessity. Note that assumption (2) is satisfied when N is a stopping time for the sequence (Xn)n∈ℕ. Assumption (3) is of more technical nature, implying absolute convergence and therefore allowing arbitrary rearrangement of an infinite series in the proof.
If assumption (5) is satisfied, then assumption (3) can be strengthened to the simpler condition
- 6. there exists a real constant C such that E[|Xn| 1{N ≥ n}] ≤ C P(N ≥ n) for all natural numbers n.
Indeed, using assumption (6),
and the last series equals the expectation of N [Proof], which is finite by assumption (5). Therefore, (5) and (6) imply assumption (3).
Assume in addition to (1) and (5) that
- 7. N is independent of the sequence (Xn)n∈ℕ and
- 8. there exists a constant C such that E[|Xn|] ≤ C for all natural numbers n.
Then all the assumptions (1), (2), (5) and (6), hence also (3) are satisfied. In particular, the conditions (4) and (8) are satisfied if
- 9. the random variables (Xn)n∈ℕ all have the same distribution.
Note that the random variables of the sequence (Xn)n∈ℕ don't need to be independent.
The interesting point is to admit some dependence between the random number N of terms and the sequence (Xn)n∈ℕ. A standard version is to assume (1), (5), (8) and the existence of a filtration (Fn)n∈ℕ0 such that
- 10. N is a stopping time with respect to the filtration, and
- 11. Xn and Fn–1 are independent for every n ∈ ℕ.
Then (10) implies that the event {N ≥ n} = {N ≤ n – 1}c is in Fn–1, hence by (11) independent of Xn. This implies (2), and together with (8) it implies (6).
For convenience (see the proof below using the optional stopping theorem) and to specify the relation of the sequence (Xn)n∈ℕ and the filtration (Fn)n∈ℕ0, the following additional assumption is often imposed:
- 12. the sequence (Xn)n∈ℕ is adapted to the filtration (Fn)n∈ℕ, meaning the Xn is Fn-measurable for every n ∈ ℕ.
Note that (11) and (12) together imply that the random variables (Xn)n∈ℕ are independent.
Application
An application is in actuarial science when considering the total claim amount follows a compound Poisson process
within a certain time period, say one year, arising from a random number N of individual insurance claims, whose sizes are described by the random variables (Xn)n∈ℕ. Under the above assumptions, Wald's equation can be used to calculate the expected total claim amount when information about the average claim number per year and the average claim size is available. Under stronger assumptions and with more information about the underlying distributions, Panjer's recursion can be used to calculate the distribution of SN.
Examples
Example with dependent terms
Let N be an integrable, ℕ0-valued random variable, which is independent of the integrable, real-valued random variable Z with E[Z] = 0. Define Xn = (–1)n Z for all n ∈ ℕ. Then assumptions (1), (5), (7), and (8) with C := E[|Z|] are satisfied, hence also (2) and (6), and Wald's equation applies. If the distribution of Z is not symmetric, then (9) does not hold. Note that, when Z is not almost surely equal to the zero random variable, then (11) and (12) cannot hold simultaneously for any filtration (Fn)n∈ℕ, because Z cannot be independent of itself as E[Z 2] = (E[Z])2 = 0 is impossible.
Example where the number of terms depends on the sequence
Let (Xn)n∈ℕ be a sequence of independent, symmetric, and {–1, +1}-valued random variables. For every n ∈ ℕ let Fn be the σ-algebra generated by X1, . . . , Xn and define N = n when Xn is the first random variable taking the value +1. Note that P(N = n) = 1/2n, hence E[N] < ∞ by the ratio test. The assumptions (1), (5) and (9), hence (4) and (8) with C = 1, (10), (11), and (12) hold, hence also (2), and (6) and Wald's equation applies. However, (7) does not hold, because N is defined in terms of the sequence (Xn)n∈ℕ. Intuitively, one might expect to have E[SN] > 0 in this example, because the summation stops right after a one, thereby apparently creating a positive bias. However, Wald's equation shows that this intuition is misleading.
Counterexamples
A counterexample illustrating the necessity of assumption (2)
Consider a sequence (Xn)n∈ℕ of i.i.d. random variables, taking each of the two values 0 and 1 with probability ½ (actually, only X1 is needed in the following). Define N = 1 – X1. Then SN is identically equal to zero, hence E[SN] = 0, but E[X1] = ½ and E[N] = ½ and therefore Wald's equation does not hold. Indeed, the assumptions (1), (3), (4) and (5) are satisfied, however, the equation in assumption (2) holds for all n ∈ ℕ except for n = 1.
A counterexample illustrating the necessity of assumption (3)
Very similar to the second example above, let (Xn)n∈ℕ be a sequence of independent, symmetric random variables, where Xn takes each of the values 2n and –2n with probability ½. Let N be the first n ∈ ℕ such that Xn = 2n. Then, as above, N has finite expectation, hence assumption (5) holds. Since E[Xn] = 0 for all n ∈ ℕ, assumptions (1) and (4) hold. However, since SN = 1 almost surely, Wald's equation cannot hold.
Since N is a stopping time with respect to the filtration generated by (Xn)n∈ℕ, assumption (2) holds, see above. Therefore, only assumption (3) can fail, and indeed, since
and therefore P(N ≥ n) = 1/2n–1 for every n ∈ ℕ, it follows that
A proof using the optional stopping theorem
Assume (1), (5), (8), (10), (11) and (12). Using assumption (1), define the sequence of random variables
Assumption (11) implies that the conditional expectation of Xn given Fn–1 equals E[Xn] almost surely for every n ∈ ℕ, hence (Mn)n∈ℕ0 is a martingale with respect to the filtration (Fn)n∈ℕ0 by assumption (12). Assumptions (5), (8) and (10) make sure that we can apply the optional stopping theorem, hence MN = SN – TN is integrable and
-
![\operatorname{E}[S_N-T_N] = \operatorname{E}[M_0] = 0.](../I/m/39bd8d43ba8dc6c7db1654e9a3a8ca6c.png)
(13)
Due to assumption (8),
and due to assumption (5) this upper bound is integrable. Hence we can add the expectation of TN to both sides of Equation (13) and obtain by linearity
Remark: Note that this proof does not cover the above example with dependent terms.
General proof
This proof uses only Lebesgue's monotone and dominated convergence theorems. We prove the statement as given above in three steps.
Step 1: Integrability of the random sum SN
We first show that the random sum SN is integrable. Define the partial sums
-
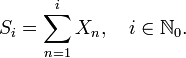
(14)
Since N takes its values in ℕ0 and since S0 = 0, it follows that
The Lebesgue monotone convergence theorem implies that
By the triangle inequality,
Using this upper estimate and changing the order of summation (which is permitted because all terms are non-negative), we obtain
-
![\operatorname{E}[|S_N|]\le\sum_{n=1}^\infty\sum_{i=n}^\infty\operatorname{E}[|X_n|\,1_{\{N=i\}}]\le\sum_{n=1}^\infty\operatorname{E}[|X_n|\,1_{\{N\ge n\}}],](../I/m/3b410c817056acbdd862546d63becb09.png)
(15)
where the second inequality follows using the monotone convergence theorem. By assumption (3), the infinite sequence on the right-hand side of (15) converges, hence SN is integrable.
Step 2: Integrability of the random sum TN
We now show that the random sum TN is integrable. Define the partial sums
-
![T_i=\sum_{n=1}^i\operatorname{E}[X_n],\quad i\in{\mathbb N}_0,](../I/m/d3b09d0b0bfc63c8b78c3cf1cdc8462d.png)
(16)
of real numbers. Since N takes its values in ℕ0 and since T0 = 0, it follows that
The Lebesgue monotone convergence theorem implies that
By the triangle inequality,
Using this upper estimate and changing the order of summation (which is permitted because all terms are non-negative), we obtain
-
![\operatorname{E}[|T_N|]\le\sum_{n=1}^\infty\bigl|\!\operatorname{E}[X_n]\bigr|\underbrace{\sum_{i=n}^\infty\operatorname{P}(N=i)}_{=\,\operatorname{P}(N\ge n)},](../I/m/da25c38c1f4c5c75d48f1a3a0200c9e7.png)
(17)
By assumption (2),
Substituting this into (17) yields
which is finite by assumption (3), hence TN is integrable.
Step 3: Proof of the identity
To prove Wald's equation, we essentially go through the same steps again without the absolute value, making use of the integrability of the random sums SN and TN in order to show that they have the same expectation. Using the dominated convergence theorem with dominating random variable |SN| and the definition of the partial sum Si given in (14), it follows that
Due to the absolute convergence proved in (15) above using assumption (3), we may rearrange the summation and obtain that
where we used assumption (1) and the dominated convergence theorem with dominating random variable |Xn| for the second equality. Due to assumption (2) and the σ-additivity of the probability measure,
Substituting this result into the previous equation, rearranging the summation (which is permitted due to absolute convergence, see (15) above), using linearity of expectation and the definition of the partial sum Ti of expectations given in (16),
By using dominated convergence again with dominating random variable |TN|,
If assumptions (4) and (5) are satisfied, then by linearity of expectation,
This completes the proof.
Further generalizations
- Wald's equation can be transferred to Rd-valued random variables (Xn)n∈ℕ by applying the one-dimensional version to every component.
- If (Xn)n∈ℕ are Bochner-integrable random variables taking values in a Banach space, then the general proof above can be adjusted accordingly.
See also
Notes
- ↑ Janssen, Jacques; Manca, Raimondo (2006). "Renewal Theory". Applied Semi-Markov Processes. Springer. pp. 45–104. doi:10.1007/0-387-29548-8_2. ISBN 0-387-29547-X.
- ↑ Thomas Bruss, F.; Robertson, J. B. (1991). "'Wald's Lemma' for Sums of Order Statistics of i.i.d. Random Variables". Advances in Applied Probability 23 (3): 612–623. doi:10.2307/1427625. JSTOR 1427625.
References
- Wald, Abraham (September 1944). "On cumulative sums of random variables". The Annals of Mathematical Statistics 15 (3): 283–296. doi:10.1214/aoms/1177731235. JSTOR 2236250. MR 10927. Zbl 0063.08122.
- Wald, Abraham (1945). "Some generalizations of the theory of cumulative sums of random variables". The Annals of Mathematical Statistics 16 (3): 287–293. doi:10.1214/aoms/1177731092. JSTOR 2235707. MR 13852. Zbl 0063.08129.
- Chan, Hock Peng; Fuh, Cheng-Der; Hu, Inchi (2006). "Multi-armed bandit problem with precedence relations". IMS Lecture Notes: Time Series and Related Topics (SUBSCRIPTION REQUIRED) 52: 223–235. arXiv:math/0702819. doi:10.1214/074921706000001067.
![\operatorname{E}[X_1+\dots+X_N]=\operatorname{E}[N] \operatorname{E}[X_1]\,.](../I/m/080126e7be68a2cd0733de31384bf800.png)
![\operatorname{E}[N] \operatorname{E}[X] = \frac{1+2+3+4+5+6}6\cdot\frac{1+2+3+4+5+6}6 = \frac{441}{36} = 12.25\,.](../I/m/a01a08e331f088870cd0dd43f239d015.png)
![\sum_{n=1}^\infty\operatorname{E}\!\bigl[|X_n|1_{\{N\ge n\}}\bigr]<\infty.](../I/m/3479d697c96b36af9c6ca7ed2ed0cad9.png)
![S_N:=\sum_{n=1}^NX_n,\qquad T_N:=\sum_{n=1}^N\operatorname{E}[X_n]](../I/m/3505d779b8286e4285ab9506b1d2a5ef.png)
![\operatorname{E}[S_N]=\operatorname{E}[T_N].](../I/m/85d7d3d79c8cb14e44b8f05e4cfe2b9c.png)
![\operatorname{E}[S_N]=\operatorname{E}[N]\, \operatorname{E}[X_1].](../I/m/192ea763e94d8b7d06e6b6916dcc49a3.png)
![\sum_{n=1}^\infty\operatorname{E}\!\bigl[|X_n|1_{\{N\ge n\}}\bigr]\le
C\sum_{n=1}^\infty\operatorname{P}(N\ge n),](../I/m/424927c83e08a568f4adffbf4405bc3f.png)
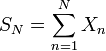
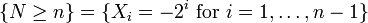
![\sum_{n=1}^\infty\operatorname{E}\!\bigl[|X_n|1_{\{N\ge n\}}\bigr]
=\sum_{n=1}^\infty 2^n\,\operatorname{P}(N\ge n)
=\sum_{n=1}^\infty 2=\infty.](../I/m/ef1588442bb4a8a1a8141aa490f20a85.png)
![M_n = \sum_{i=1}^n (X_i - \operatorname{E}[X_i]),\quad n\in{\mathbb N}_0.](../I/m/103a3de4602ea57a6503337b3e44ab5d.png)
![|T_N|=\biggl|\sum_{i=1}^N\operatorname{E}[X_i]\biggr| \le \sum_{i=1}^N\operatorname{E}[|X_i|]\le CN,](../I/m/180d7f19f5f45c0e89864f1cd1012f7b.png)
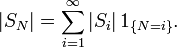
![\operatorname{E}[|S_N|]=\sum_{i=1}^\infty\operatorname{E}[|S_i|\,1_{\{N=i\}}].](../I/m/4c0afbd9b0682ffc4b5f156ca1dc0150.png)
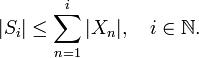
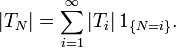
![\operatorname{E}[|T_N|]=\sum_{i=1}^\infty |T_i|\operatorname{P}(N=i).](../I/m/fdeb4288067be01db9368f6abeea2930.png)
![|T_i|\le\sum_{n=1}^i\bigl|\!\operatorname{E}[X_n]\bigr|,\quad i\in{\mathbb N}.](../I/m/5828d711ccb010855ffbd6e350db69bd.png)
![\bigl|\!\operatorname{E}[X_n]\bigr|\operatorname{P}(N\ge n)
=\bigl|\!\operatorname{E}[X_n1_{\{N\ge n\}}]\bigr|
\le\operatorname{E}[|X_n|1_{\{N\ge n\}}],\quad n\in{\mathbb N}.](../I/m/55eefd6b5f8217a839af37f80c1c5ec7.png)
![\operatorname{E}[|T_N|]\le\sum_{n=1}^\infty\operatorname{E}[|X_n|1_{\{N\ge n\}}],](../I/m/a51d1dd9ade0b23b2c3f7fcd53a26a11.png)
![\operatorname{E}[S_N]=\sum_{i=1}^\infty\operatorname{E}[S_i1_{\{N=i\}}]
=\sum_{i=1}^\infty\sum_{n=1}^i\operatorname{E}[X_n1_{\{N=i\}}].](../I/m/e8ca5116395e10abe50b0e460f34b298.png)
![\operatorname{E}[S_N]=\sum_{n=1}^\infty\sum_{i=n}^\infty\operatorname{E}[X_n1_{\{N=i\}}]=\sum_{n=1}^\infty\operatorname{E}[X_n1_{\{N\ge n\}}],](../I/m/1cd400f04b5aae14e7753d5eacc055d0.png)
![\begin{align}\operatorname{E}[X_n1_{\{N\ge n\}}] &=\operatorname{E}[X_n]\operatorname{P}(N\ge n)\\
&=\operatorname{E}[X_n]\sum_{i=n}^\infty\operatorname{P}(N=i)
=\sum_{i=n}^\infty\operatorname{E}\!\bigl[\operatorname{E}[X_n]1_{\{N=i\}}\bigr].\end{align}](../I/m/f29e2a5f5cae97adf3e882467d3c8f4a.png)
![\operatorname{E}[S_N]=\sum_{i=1}^\infty\sum_{n=1}^i\operatorname{E}\!\bigl[\operatorname{E}[X_n]1_{\{N=i\}}\bigr]=\sum_{i=1}^\infty\operatorname{E}[\underbrace{T_i1_{\{N=i\}}}_{=\,T_N1_{\{N=i\}}}].](../I/m/a598780fcff96a6a22a10d3a835d2fd5.png)
![\operatorname{E}[S_N]=\operatorname{E}\!\biggl[T_N\underbrace{\sum_{i=1}^\infty1_{\{N=i\}}}_{=\,1_{\{N\ge1\}}}\biggr]=\operatorname{E}[T_N].](../I/m/df4d23158c97bf38f15e2f603bd52ffb.png)
![\operatorname{E}[T_N]=\operatorname{E}\!\biggl[\sum_{n=1}^N \operatorname{E}[X_n]\biggr]=\operatorname{E}[X_1]\operatorname{E}\!\biggl[\underbrace{\sum_{n=1}^N 1}_{=\,N}\biggr]=\operatorname{E}[N]\operatorname{E}[X_1].](../I/m/6556e262242bd25f8c61bb85df70ceae.png)