Wahlquist fluid
In general relativity, the Wahlquist fluid is an exact rotating perfect fluid solution to Einstein's equation with equation of state corresponding to constant gravitational mass density.
Introduction
The Wahlquist fluid was first discovered by Hugo D. Wahlquist in 1968.[1] It is one of few known exact rotating perfect fluid solutions in general relativity. The solution reduces to the static Whittaker metric in the limit of zero rotation.
Metric
The metric of a Wahlquist fluid is given by
where
and 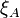 is defined by
is defined by 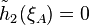 . It is a solution with equation of state
. It is a solution with equation of state 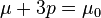 where
where 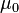 is a constant.
is a constant.
Properties
The pressure and density of the Wahlquist fluid are given by
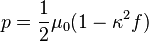
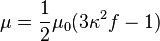
The vanishing pressure surface of the fluid is prolate, in contrast to physical rotating stars, which are oblate. It has been shown that the Wahlquist fluid can not be matched to an asymptotically flat region of spacetime [2]
References
- ↑ PhysRev.172.1291, Interior Solution for a Finite Rotating Body of Perfect Fluid, Wahlquist, Hugo D., 1968, 10.1103/PhysRev.172.1291, http://link.aps.org/doi/10.1103/PhysRev.172.1291
- ↑ M. Bradley, G. Fodor, M. Marklund and Z. Perj ́es,Class.Quantum Grav.,17, 351 (2000)
![ds^2=f(dt-\tilde{A}d\varphi)^2-r_0^2(\zeta^2+\xi^2)[\frac{d\zeta^2}{(1-\tilde{k}^2\zeta^2)\tilde{h}_1}+\frac{d\xi^2}{(1+\tilde{k}^2\xi^2)\tilde{h}_2}+\frac{\tilde{h}_1\tilde{h}_2}{\tilde{h}_1-\tilde{h}_2}d\varphi^2]](../I/m/95705315011b9e82658d15b8a77e8acf.png)
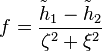
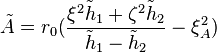
![\tilde{h}_1(\zeta)=1+\zeta^2+\frac{\zeta}{\kappa^2}[\zeta_+\frac{1}{\tilde{k}}\sqrt{1-\tilde{k}^2\zeta^2}\arcsin(\tilde{k}\zeta)]](../I/m/bd6187f2a95c565a877f952c66488af7.png)
![\tilde{h}_2(\xi)=1-\xi^2-\frac{\xi}{\kappa^2}[\xi_-\frac{1}{\tilde{k}}\sqrt{1+\tilde{k}^2\xi^2}\sinh^{-1} (\tilde{k}\xi)]](../I/m/8256a5ca0b42954ad244fcc967245368.png)