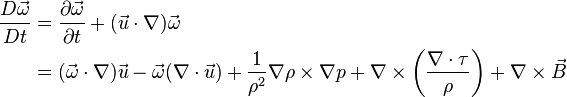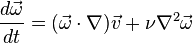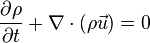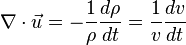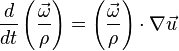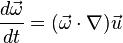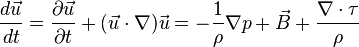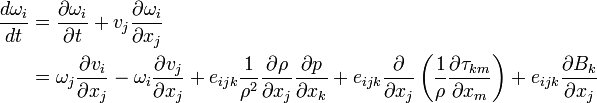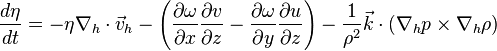Vorticity equation

The vorticity equation of fluid dynamics describes evolution of the vorticity ω→ of a particle of a fluid as it moves with its flow, that is, the local rotation of the fluid (in terms of vector calculus this is the curl of the flow velocity). The equation is:

\begin{align} \frac{D\vec\omega}{Dt} &= \frac{\partial \vec \omega}{\partial t} + (\vec u \cdot \nabla) \vec \omega \\ &= (\vec \omega \cdot \nabla) \vec u - \vec \omega (\nabla \cdot \vec u) + \frac{1}{\rho^2}\nabla \rho \times \nabla p + \nabla \times \left( \frac{\nabla \cdot \tau}{\rho} \right) + \nabla \times \vec B \end{align}

where d/dt the total time derivative operator, also denoted by in capital D notation as D/Dt, u→ is the flow velocity, ρ is the local fluid density, p is the local pressure, τ is the viscous stress tensor and B→ represents the sum of the external body forces. The first source term on the right hand side represents vortex stretching. The equation is valid in the absence of any concentrated torques and line forces, for a compressible Newtonian fluid.

In the case of incompressible (i.e. low Mach number) and isotropic fluids, with conservative body forces, the equation simplifies to the vorticity transport equation

{d\vec{\omega} \over dt} = (\vec{\omega} \cdot \nabla) \vec{v} + \nu \nabla^2 \vec{\omega}

where ν is the kinematic viscosity and ∇2 is the Laplace operator.

Physical Interpretation

\frac{\partial \rho}{\partial t} + \nabla \cdot(\rho \vec u) = 0
or
\nabla \cdot \vec u = -\frac{1}{\rho} \frac{d \rho}{dt} = \frac{1}{v} \frac{dv}{dt}
where v = 1/ρ is the specific volume of the fluid element. One can think of ∇→ ∙ u→ as a measure of flow compressibility. Sometimes the negative sign is included in the term.

Simplifications

Thus for an inviscid, barotropic fluid with conservative body forces, the vorticity equation simplifies to

\frac{d}{dt} \left( \frac{\vec \omega}{\rho} \right) = \left( \frac{\vec\omega}{\rho} \right) \cdot \nabla \vec u

Alternately, in case of incompressible, inviscid fluid with conservative body forces,

\frac{d \vec \omega}{dt} = (\vec \omega \cdot \nabla) \vec u

For a brief review of additional cases and simplifications, see also.[1]

Derivation

The vorticity equation can be derived from the Navier-Stokes equation for the conservation of angular momentum. In the absence of any concentrated torques and line forces, one obtains

\frac{d \vec u}{d t} = \frac{\partial \vec u}{\partial t} + (\vec u \cdot \nabla) \vec u = - \frac{1}{\rho} \nabla p + \vec B + \frac{\nabla \cdot \tau}{\rho}

Now, vorticity is defined as the curl of the flow velocity vector. Taking curl of momentum equation yields the desired equation.

The following identities are useful in derivation of the equation,

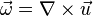
\vec \omega = \nabla \times \vec u
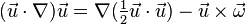
(\vec u \cdot \nabla) \vec u = \nabla (\tfrac{1}{2} \vec u \cdot \vec u) - \vec u \times \vec \omega
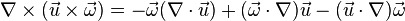
\nabla \times (\vec u \times \vec \omega ) = -\vec \omega (\nabla \cdot \vec u) + (\vec \omega \cdot \nabla ) \vec u - (\vec u \cdot \nabla) \vec \omega
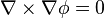\nabla \times \nabla \phi = 0 , where ϕ is any scalar field.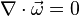
\nabla \cdot \vec \omega = 0

Tensor notation

The vorticity equation can be expressed in tensor notation using Einstein's summation convention and the Levi-Civita symbol eijk:

\begin{align} \frac{d\omega_i}{dt} &= \frac{\partial \omega_i}{\partial t} + v_j \frac{\partial \omega_i}{\partial x_j} \\ &= \omega_j \frac{\partial v_i}{\partial x_j} - \omega_i \frac{\partial v_j}{\partial x_j} + e_{ijk}\frac{1}{\rho^2}\frac{\partial \rho}{\partial x_j}\frac{\partial p}{\partial x_k} + e_{ijk}\frac{\partial}{\partial x_j}\left(\frac{1}{\rho}\frac{\partial \tau_{km}}{\partial x_m}\right) + e_{ijk}\frac{\partial B_k }{\partial x_j} \end{align}

In specific sciences

Atmospheric sciences

In the atmospheric sciences, the vorticity equation can be stated in terms of the absolute vorticity of air with respect to an inertial frame, or of the vorticity with respect to the rotation of the Earth. The absolute version is

\frac{d \eta}{d t} = -\eta \nabla_h \cdot\vec{v}_h - \left( \frac{\partial \omega}{\partial x} \frac{\partial v}{\partial z} - \frac{\partial \omega}{\partial y} \frac{\partial u}{\partial z} \right) - \frac{1}{\rho^2} \vec{k} \cdot ( \nabla_h p \times \nabla_h \rho )

Here, η is the polar (z) component of the vorticity, ρ is the atmospheric density, u, u, and ω are the components of wind velocity, and ∇h is the 2-dimensional (i.e. horizontal-component-only) del.

See also

References

  1. ↑ K. P. Burr, Marine Hydrodynamics, Lecture 9, MIT Lectures. http://web.mit.edu/2.20/www/lectures/Lecture-2014/lecture9-2014.pdf''