Von Neumann cellular automaton

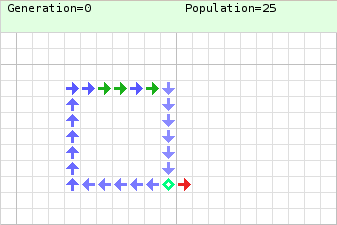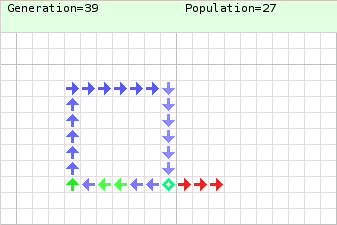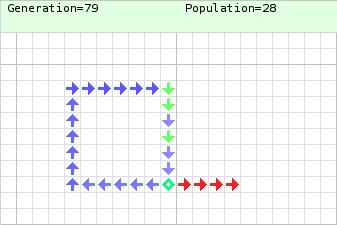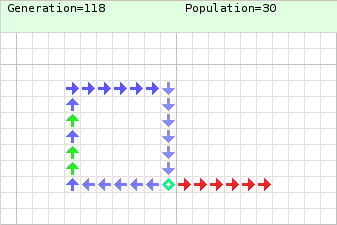
Von Neumann cellular automata are the original expression of cellular automata, the development of which were prompted by suggestions made to John von Neumann by his close friend and fellow mathematician Stanislaw Ulam. Their original purpose was to provide insight into the logical requirements for machine self-replication and were used in von Neumann's universal constructor.

Nobili's cellular automaton is a variation of von Neumann's cellular automaton, augmented with the ability for confluent cells to cross signals and store information. The former requires an extra three states, hence Nobili's cellular automaton has 32 states, rather than 29. Hutton's cellular automaton is yet another variation, which allows a loop of data, analogous to Langton's loops, to replicate.

Definition

Configuration

In general, cellular automata (CA) constitute an arrangement of finite state automata (FSA) that sit in positional relationships between one another, each FSA exchanging information with those other FSAs to which it is positionally adjacent. In von Neumann's cellular automaton, the finite state machines (or cells) are arranged in a two-dimensional Cartesian grid, and interface with the surrounding four cells. As von Neumann's cellular automaton was the first example to use this arrangement, it is known as the von Neumann neighbourhood.

The set of FSAs define a cell space of infinite size. All FSAs are identical in terms of state-transition function, or rule-set.

The neighborhood (a grouping function) is part of the state-transition function, and defines for any cell the set of other cells upon which the state of that cell depends.

All cells transition state synchronously, in step with a universal "clock" as in a synchronous digital circuit.

States

Each FSA of the von Neumann cell space can accept any of the 29 states of the rule-set. The rule-set is grouped into five orthogonal subsets. Each state includes the colour of the cell in the cellular automata program Golly in (red, green, blue). They are

a ground state U (48, 48, 48)
the transition or sensitised states (in 8 substates)
1. S (newly sensitised) (255, 0, 0)
2. S₀ - (sensitised, having received no input for one cycle) (255, 125, 0)
3. S₀₀ - (sensitised, having received no input for two cycles) (255, 175, 50)
4. S₀₀₀ - (sensitised, having received no input for three cycles) (251, 255, 0)
5. S₀₁ - (sensitised, having received no input for one cycle and then an input for one cycle) (255, 200, 75)
6. S₁ - (sensitised, having received an input for one cycle) (255, 150, 25)
7. S₁₀ - (sensitised, having received an input for one cycle and then no input for one cycle) (255, 255, 100)
8. S₁₁ - (sensitised, having received input for two cycles) (255, 250, 125)
the confluent states (in 4 states of excitation)
1. C₀₀ - quiescent (and will also be quiescent next cycle) (0, 255, 128)
2. C₀₁ - next-excited (now quiescent, but will be excited next cycle) (33, 215, 215)
3. C₁₀ - excited (but will be quiescent next cycle) (255, 255, 128)
4. C₁₁ - excited next-excited (currently excited and will be excited next cycle) (255, 128, 64)
the ordinary transmission states (in 4 directions, excited or quiescent, making 8 states)
1. North-directed (excited and quiescent) (36, 200, 36) (106, 106, 255)
2. South-directed (excited and quiescent) (106, 255, 106) (139, 139, 255)
3. West-directed (excited and quiescent) (73, 255, 73) (122, 122, 255)
4. East-directed (excited and quiescent) (27, 176, 27) (89, 89, 255)
the special transmission states (in 4 directions, excited or quiescent, making 8 states)
1. North-directed (excited and quiescent) (191, 73, 255) (255, 56, 56)
2. South-directed (excited and quiescent) (203, 106, 255) (255, 89, 89)
3. West-directed (excited and quiescent) (197, 89, 255) (255, 73, 73)
4. East-directed (excited and quiescent) (185, 56, 255) (235, 36, 36)

"Excited" states carry data, at the rate of one bit per state transition step.

Note that confluent states have the property of a one-cycle delay, thus effectively holding two bits of data at any given time.

Transmission state rules

The flow of bits between cells is indicated by the direction property. The following rules apply:

Transmission states apply the OR operator to inputs, meaning a cell in a transmission state (ordinary or special) will be excited at time t+1 if any of the inputs pointing to it is excited at time t
Data passes from cell A in an ordinary transmission state to an adjacent cell B in an ordinary transmission state, according to the direction property of A (unless B is also directed towards A, in which case the data disappears).
Data passes from cell A in a special transmission state to an adjacent cell B in a special transmission state, according to the same rules as for ordinary transmission states.
The two subsets of transmission states, ordinary and special, are mutually antagonistic:
- Given a cell A at time t in the excited ordinary transmission state
- pointing to a cell B in any special transmission state
- at time t+1 cell B will become the ground state. The special transmission cell has been "destroyed".
- a similar sequence will occur in the case of a cell in the special transmission state "pointing" to a cell in the ordinary transmission state

Confluent state rules

The following specific rules apply to confluent states:

Confluent states do not pass data between each other.
Confluent states take input from one or more ordinary transmission states, and deliver output to transmission states, ordinary and special, that are not directed toward the confluent state.
Data are not transmitted against the transmission state direction property.
Data held by a confluent state is lost if that state has no adjacent transmission state that is also not pointed at the confluent state.
Thus, confluent-state cells are used as "bridges" from transmission lines of ordinary- to special-transmission state cells.
The confluent state applies the AND operator to inputs, only "saving" an excited input if all potential inputs are excited simultaneously.
Confluent cells delay signals by one generation more than OTS cells; this is necessary due to parity constraints.

Construction rules

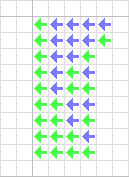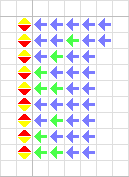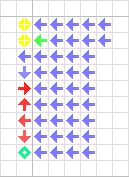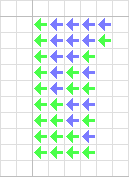
Initially, much of the cell-space, the universe of the cellular automaton, is "blank," consisting of cells in the ground state U. When given an input excitation from a neighboring ordinary- or special transmission state, the cell in the ground state becomes "sensitised," transitioning through a series of states before finally "resting" at a quiescent transmission or confluent state.

The choice of which destination state the cell will reach is determined by the sequence of input signals. Therefore, the transition/sensitised states can be thought of as the nodes of a bifurcation tree leading from the ground-state to each of the quiescent transmission and confluent states.

In the following tree, the sequence of inputs is shown as a binary string after each step:

a cell in the ground state U, given an input, will transition to the S (newly sensitised) state in the next cycle (1)
a cell in the S state, given no input, will transition into the S₀ state (10)
- a cell in the S₀ state, given no input, will transition into the S₀₀ state (100)
  - a cell in the S₀₀ state, given no input, will transition into the S₀₀₀ state (1000)
    - a cell in the S₀₀₀ state, given no input, will transition into the east-directed ordinary transmission state (10000)
    - a cell in the S₀₀₀ state, given an input, will transition into the north-directed ordinary transmission state (10001)
  - a cell in the S₀₀ state, given an input, will transition into the west-directed ordinary transmission state (1001)
- a cell in the S₀ state, given an input, will transition into the S₀₁ state (101)
  - a cell in the S₀₁ state, given no input, will transition into the south-directed ordinary transmission state (1010)
  - a cell in the S₀₁ state, given an input, will transition into the east-directed special transmission state (1011)
a cell in the S state, given an input, will transition into the S₁ state (11)
- a cell in the S₁ state, given no input, will transition into the S₁₀ state (110)
  - a cell in the S₁₀ state, given no input, will transition into the north-directed special transmission state (1100)
  - a cell in the S₁₀ state, given an input, will transition into the west-directed special transmission state (1101)
- a cell in the S₁ state, given an input, will transition into the S₁₁ state (111)
  - a cell in the S₁₁ state, given no input, will transition into the south-directed special transmission state (1110)
  - a cell in the S₁₁ state, given an input, will transition into the quiescent confluent state C₀₀ (1111)

Note that:

one more cycle of input (four after the initial sensitization) is required to build the east- or north-directed ordinary transmission state than any of the other states (which require three cycles of input after the initial sensitization),
the "default" quiescent state resulting in construction is the east-directed ordinary transmission state- which requires an initial sensitization input, and then four cycles of no input.

Destruction rules

Roughly 4000 bits of data in a curled up "tape" constructing a complex pattern. This uses a 32-state variation of von Neumann cellular automata known as Hutton32.

An input into a confluent-state cell from a special-transmission state cell will result in the confluent state cell being reduced back to the ground state.
Likewise, an input into an ordinary transmission-state cell from a special-transmission state cell will result in the ordinary-transmission state cell being reduced back to the ground state.
Conversely, an input into a special transmission-state cell from an ordinary-transmission state cell will result in the special-transmission state cell being reduced back to the ground state.

References

Von Neumann, J. and A. W. Burks (1966). Theory of self-reproducing automata. Urbana, University of Illinois Press.

External links

Golly - supports von Neumann's CA along with the Game of Life, and other rulesets.