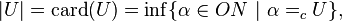Von Neumann cardinal assignment
The von Neumann cardinal assignment is a cardinal assignment which uses ordinal numbers. For a well-ordered set U, we define its cardinal number to be the smallest ordinal number equinumerous to U. More precisely:
where ON is the class of ordinals. This ordinal is also called the initial ordinal of the cardinal.
That such an ordinal exists and is unique is guaranteed by the fact that U is well-orderable and that the class of ordinals is well-ordered, using the axiom of replacement. With the full axiom of choice, every set is well-orderable, so every set has a cardinal; we order the cardinals using the inherited ordering from the ordinal numbers. This is readily found to coincide with the ordering via ≤c. This is a well-ordering of cardinal numbers.
Initial ordinal of a cardinal
Each ordinal has an associated cardinal, its cardinality, obtained by simply forgetting the order. Any well-ordered set having that ordinal as its order type has the same cardinality. The smallest ordinal having a given cardinal as its cardinality is called the initial ordinal of that cardinal. Every finite ordinal (natural number) is initial, but most infinite ordinals are not initial. The axiom of choice is equivalent to the statement that every set can be well-ordered, i.e. that every cardinal has an initial ordinal. In this case, it is traditional to identify the cardinal number with its initial ordinal, and we say that the initial ordinal is a cardinal.
The α-th infinite initial ordinal is written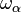 
. Its cardinality is written ℵα (the α-th aleph number). For example, the cardinality of ω0 = ω is ℵ0, which is also the cardinality of ω2, ωω, and ε0 (all are countable ordinals). So (assuming the axiom of choice) we identify ωα with ℵα, except that the notation ℵα is used for writing cardinals, and ωα for writing ordinals. This is important because arithmetic on cardinals is different from arithmetic on ordinals, for example ℵα2 = ℵα whereas ωα2 > ωα. Also, ω1 is the smallest uncountable ordinal (to see that it exists, consider the set of equivalence classes of well-orderings of the natural numbers; each such well-ordering defines a countable ordinal, and ω1 is the order type of that set), ω2 is the smallest ordinal whose cardinality is greater than ℵ1, and so on, and ωω is the limit of ωn for natural numbers n (any limit of cardinals is a cardinal, so this limit is indeed the first cardinal after all the ωn).
Infinite initial ordinals are limit ordinals. Using ordinal arithmetic, α < ωβ implies α+ωβ = ωβ, and 1 ≤ α < ωβ implies α·ωβ = ωβ, and 2 ≤ α < ωβ implies αωβ = ωβ. Using the Veblen hierarchy, β ≠ 0 and α < ωβ imply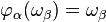 
and Γωβ = ωβ. Indeed, one can go far beyond this. So as an ordinal, an infinite initial ordinal is an extremely strong kind of limit.
See also
References
- Y.N. Moschovakis Notes on Set Theory (1994 Springer) p. 198