Vitali convergence theorem
In real analysis and measure theory, the Vitali convergence theorem, named after the Italian mathematician Giuseppe Vitali, is a generalization of the better-known dominated convergence theorem of Henri Lebesgue. It is a strong condition that depends on uniform integrability. It is useful when a dominating function cannot be found for the sequence of functions in question; when such a dominating function can be found, Lebesgue's theorem follows as a special case of Vitali's.
Statement of the theorem[1]
Let 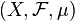 be a positive measure space. If
be a positive measure space. If
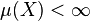
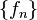 is uniformly integrable
is uniformly integrable 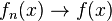 a.e. as
a.e. as 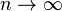 and
and 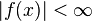 a.e.
a.e.
then the following hold:
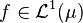
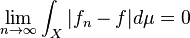 .
.
Outline of Proof
- For proving statement 1, we use Fatou's lemma:
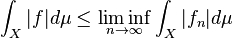
- Using uniform integrability, we have
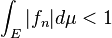 where
where 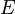 is a set such that
is a set such that 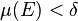
- By Egorov's theorem,
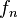 converges uniformly on the set
converges uniformly on the set 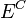 .
. 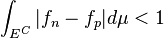 for a large
for a large 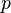 and
and 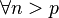 . Using triangle inequality,
. Using triangle inequality, 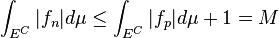
- Plugging the above bounds on the RHS of Fatou's lemma gives us statement 1.
- Using uniform integrability, we have
- For statement 2, use
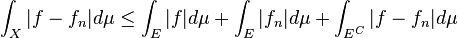 , where
, where 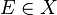 and
and 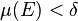 .
.
- The terms in the RHS are bounded respectively using Statement 1, uniform integrability of
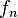 and Egorov's theorem for all
and Egorov's theorem for all 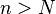 .
.
- The terms in the RHS are bounded respectively using Statement 1, uniform integrability of
Converse of the theorem[1]
Let 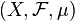 be a positive measure space. If
be a positive measure space. If
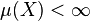 ,
, 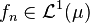 and
and 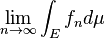 exists for every
exists for every 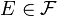
then 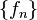 is uniformly integrable.
is uniformly integrable.
Citations
References
- Folland, Gerald B. (1999). Real analysis. Pure and Applied Mathematics (New York) (Second edition ed.). New York: John Wiley & Sons Inc. pp. xvi+386. ISBN 0-471-31716-0. MR 1681462
- Rosenthal, Jeffrey S. (2006). A first look at rigorous probability theory (Second edition ed.). Hackensack, NJ: World Scientific Publishing Co. Pte. Ltd. pp. xvi+219. ISBN 978-981-270-371-2. MR 2279622