Vibrational partition function
The vibrational partition function traditionally refers to the component of the canonical partition function resulting from the vibrational degrees of freedom of a system. The vibrational partition function is only well-defined in model systems where the vibrational motion is relatively uncoupled with the system's other degrees of freedom.
Approximations
Quantum Harmonic Oscillator
The most common approximation to the vibrational partition function uses a model in which the vibrational eigenmodes or vibrational normal modes of the system are considered to be a set of uncoupled quantum harmonic oscillators. It is a first order approximation to the partition function which allows one to calculate the contribution of the vibrational degree of freedom of molecules towards thermodynamic variables. A quantum harmonic oscillator has an energy spectrum characterized by:
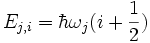
where j is an index representing the vibrational mode, and i is the quantum number for each energy level of the jth vibrational mode. The vibrational partition function is then calculated as:
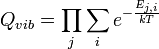
See also
| ||||||||||||||||||||||||||||||||||||||