Vertical vector field

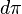In differential geometry, a vertical vector field is a vector field on a principal G-bundle $\pi: P \to M$ that is in the kernel of $d\pi$ at each point of P.^[1] More generally, the projection $\pi: P \to M$ needs only to be a fibered manifold, i.e., a surjective submersion.

Notes

↑ Kolář, Ivan; Michor, Peter; Slovák, Jan (1993), Natural operators in differential geometry (PDF), Springer-Verlag, p. 77

References

Kolář, Ivan; Michor, Peter; Slovák, Jan (1993), Natural operators in differential geometry (PDF), Springer-Verlag
Krupka, Demeter; Janyška, Josef (1990), Lectures on differential invariants, Univerzita J. E. Purkyně V Brně, ISBN 80-210-0165-8
Saunders, D.J. (1989), The geometry of jet bundles, Cambridge University Press, ISBN 0-521-36948-7

Vertical vector field

See also

Notes

References