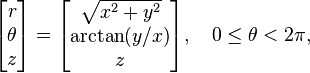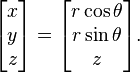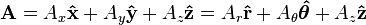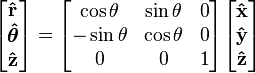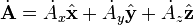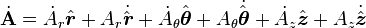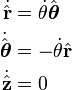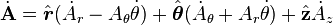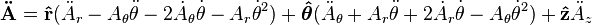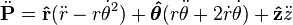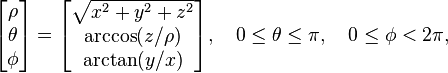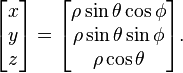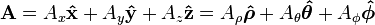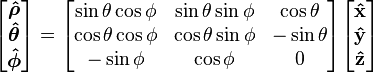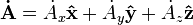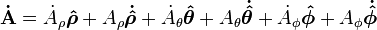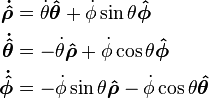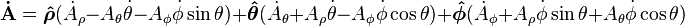Vector fields in cylindrical and spherical coordinates

Spherical coordinates (r, θ, φ) as commonly used in physics: radial distance r, polar angle θ (theta), and azimuthal angle φ (phi). The symbol ρ (rho) is often used instead of r.

NOTE: This page uses common physics notation for spherical coordinates, in which 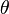\theta is the angle between the z axis and the radius vector connecting the origin to the point in question, while 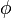\phi is the angle between the projection of the radius vector onto the x-y plane and the x axis. Several other definitions are in use, and so care must be taken in comparing different sources.[1]

Cylindrical coordinate system

Vector fields

Vectors are defined in cylindrical coordinates by (r, θ, z), where

(r, θ, z) is given in cartesian coordinates by:

\begin{bmatrix} r \\ \theta \\ z \end{bmatrix} = \begin{bmatrix} \sqrt{x^2 + y^2} \\ \operatorname{arctan}(y / x) \\ z \end{bmatrix},\ \ \ 0 \le \theta < 2\pi,

or inversely by:

\begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} r\cos\theta \\ r\sin\theta \\ z \end{bmatrix}.

Any vector field can be written in terms of the unit vectors as:

\mathbf A = A_x \mathbf{\hat x} + A_y \mathbf{\hat y} + A_z \mathbf{\hat z} = A_r \mathbf{\hat r} + A_\theta \boldsymbol{\hat \theta} + A_z \mathbf{\hat z}

The cylindrical unit vectors are related to the cartesian unit vectors by:

\begin{bmatrix}\mathbf{\hat r} \\ \boldsymbol{\hat\theta} \\ \mathbf{\hat z}\end{bmatrix} = \begin{bmatrix} \cos\theta & \sin\theta & 0 \\ -\sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \mathbf{\hat x} \\ \mathbf{\hat y} \\ \mathbf{\hat z} \end{bmatrix}

Time derivative of a vector field

To find out how the vector field A changes in time we calculate the time derivatives. For this purpose we use Newton's notation for the time derivative (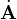\dot{\mathbf{A}}). In cartesian coordinates this is simply:

\dot{\mathbf{A}} = \dot{A}_x \hat{\mathbf{x}} + \dot{A}_y \hat{\mathbf{y}} + \dot{A}_z \hat{\mathbf{z}}

However, in cylindrical coordinates this becomes:

\dot{\mathbf{A}} = \dot{A}_r \hat{\boldsymbol{r}} + A_r \dot{\hat{\boldsymbol{r}}} + \dot{A}_\theta \hat{\boldsymbol{\theta}} + A_\theta \dot{\hat{\boldsymbol{\theta}}} + \dot{A}_z \hat{\boldsymbol{z}} + A_z \dot{\hat{\boldsymbol{z}}}

We need the time derivatives of the unit vectors. They are given by:

\begin{align} \dot{\hat{\mathbf{r}}} & = \dot{\theta} \hat{\boldsymbol{\theta}} \\ \dot{\hat{\boldsymbol{\theta}}} & = - \dot\theta \hat{\mathbf{r}} \\ \dot{\hat{\mathbf{z}}} & = 0 \end{align}

So the time derivative simplifies to:

\dot{\mathbf{A}} = \hat{\boldsymbol{r}} (\dot{A}_r - A_\theta \dot{\theta}) + \hat{\boldsymbol{\theta}} (\dot{A}_\theta + A_r \dot{\theta}) + \hat{\mathbf{z}} \dot{A}_z

Second time derivative of a vector field

The second time derivative is of interest in physics, as it is found in equations of motion for classical mechanical systems. The second time derivative of a vector field in cylindrical coordinates is given by:

\mathbf{\ddot A} = \mathbf{\hat r} (\ddot A_r - A_\theta \ddot\theta - 2 \dot A_\theta \dot\theta - A_r \dot\theta^2) + \boldsymbol{\hat\theta} (\ddot A_\theta + A_r \ddot\theta + 2 \dot A_r \dot\theta - A_\theta \dot\theta^2) + \mathbf{\hat z} \ddot A_z

To understand this expression, we substitute A = P, where p is the vector (r, θ, z).

This means that 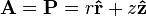\mathbf{A} = \mathbf{P} = r \mathbf{\hat r} + z \mathbf{\hat z}.

After substituting we get:

\ddot\mathbf{P} = \mathbf{\hat r} (\ddot r - r \dot\theta^2) + \boldsymbol{\hat\theta} (r \ddot\theta + 2 \dot r \dot\theta) + \mathbf{\hat z} \ddot z

In mechanics, the terms of this expression are called:

\begin{align} \ddot r \mathbf{\hat r} &= \mbox{central outward acceleration} \\ -r \dot\theta^2 \mathbf{\hat r} &= \mbox{centripetal acceleration} \\ r \ddot\theta \boldsymbol{\hat\theta} &= \mbox{angular acceleration} \\ 2 \dot r \dot\theta \boldsymbol{\hat\theta} &= \mbox{Coriolis effect} \\ \ddot z \mathbf{\hat z} &= \mbox{z-acceleration} \end{align}

See also: Centripetal force, Angular acceleration, Coriolis effect.

Spherical coordinate system

Vector fields

Vectors are defined in spherical coordinates by (ρ,θ,φ), where

(ρ,θ,φ) is given in Cartesian coordinates by:

\begin{bmatrix}\rho \\ \theta \\ \phi \end{bmatrix} = \begin{bmatrix} \sqrt{x^2 + y^2 + z^2} \\ \arccos(z / \rho) \\ \arctan(y / x) \end{bmatrix},\ \ \ 0 \le \theta \le \pi,\ \ \ 0 \le \phi < 2\pi,

or inversely by:

\begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} \rho\sin\theta\cos\phi \\ \rho\sin\theta\sin\phi \\ \rho\cos\theta\end{bmatrix}.

Any vector field can be written in terms of the unit vectors as:

\mathbf A = A_x\mathbf{\hat x} + A_y\mathbf{\hat y} + A_z\mathbf{\hat z} = A_\rho\boldsymbol{\hat \rho} + A_\theta\boldsymbol{\hat \theta} + A_\phi\boldsymbol{\hat \phi}

The spherical unit vectors are related to the cartesian unit vectors by:

\begin{bmatrix}\boldsymbol{\hat\rho} \\ \boldsymbol{\hat\theta} \\ \boldsymbol{\hat\phi} \end{bmatrix} = \begin{bmatrix} \sin\theta\cos\phi & \sin\theta\sin\phi & \cos\theta \\ \cos\theta\cos\phi & \cos\theta\sin\phi & -\sin\theta \\ -\sin\phi & \cos\phi & 0 \end{bmatrix} \begin{bmatrix} \mathbf{\hat x} \\ \mathbf{\hat y} \\ \mathbf{\hat z} \end{bmatrix}

Time derivative of a vector field

To find out how the vector field A changes in time we calculate the time derivatives. In cartesian coordinates this is simply:

\mathbf{\dot A} = \dot A_x \mathbf{\hat x} + \dot A_y \mathbf{\hat y} + \dot A_z \mathbf{\hat z}

However, in spherical coordinates this becomes:

\mathbf{\dot A} = \dot A_\rho \boldsymbol{\hat \rho} + A_\rho \boldsymbol{\dot{\hat \rho}} + \dot A_\theta \boldsymbol{\hat\theta} + A_\theta \boldsymbol{\dot{\hat\theta}} + \dot A_\phi \boldsymbol{\hat\phi} + A_\phi \boldsymbol{\dot{\hat\phi}}

We need the time derivatives of the unit vectors. They are given by:

\begin{align} \boldsymbol{\dot{\hat \rho}} &= \dot\theta \boldsymbol{\hat\theta} + \dot\phi\sin\theta \boldsymbol{\hat\phi} \\ \boldsymbol{\dot{\hat\theta}} &= - \dot\theta \boldsymbol{\hat \rho} + \dot\phi\cos\theta \boldsymbol{\hat\phi} \\ \boldsymbol{\dot{\hat\phi}} &= - \dot\phi\sin\theta \boldsymbol{\hat\rho} - \dot\phi\cos\theta \boldsymbol{\hat\theta} \end{align}

So the time derivative becomes:

\mathbf{\dot A} = \boldsymbol{\hat \rho} (\dot A_\rho - A_\theta \dot\theta - A_\phi \dot\phi \sin\theta) + \boldsymbol{\hat\theta} (\dot A_\theta + A_\rho \dot\theta - A_\phi \dot\phi \cos\theta) + \boldsymbol{\hat\phi} (\dot A_\phi + A_\rho \dot\phi \sin\theta + A_\theta \dot\phi \cos\theta)

See also

References

  1. ↑ Wolfram Mathworld, spherical coordinates