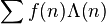Vaughan's identity

In mathematics, Vaughan's identity is an identity found by R. C. Vaughan (1977) that can be used to simplify Vinogradov's work on trigonometric sums. It can be used to estimate sums of the form

\sum f(n)\Lambda(n)

where f is some function of positive integers n, whose values in applications are often roots of unity, and Λ is the von Mangoldt function.

Vaughan's identity has been used to simplify the proof of the Bombieri–Vinogradov theorem and to study Kummer sums.

Vaughan's identity was generalized by Heath-Brown (1982).

References

Graham, S.W. (2001), "V/v130030", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Heath-Brown, D. R. (1982), "Prime numbers in short intervals and a generalized Vaughan identity", Canad. J. Math. 34 (6): 1365–1377, doi:10.4153/CJM-1982-095-9, MR 0678676
Vaughan, R.C. (1977), "Sommes trigonométriques sur les nombres premiers", C.R. Acad. Sci. Paris Sér. A 285: 981–983, MR 0498434