Variation of information
In probability theory and information theory, the variation of information or shared information distance is a measure of the distance between two clusterings (partitions of elements). It is closely related to mutual information; indeed, it is a simple linear expression involving the mutual information. Unlike the mutual information, however, the variation of information is a true metric, in that it obeys the triangle inequality. Even more, it is a universal metric, in that if any other distance measure two items close-by, then the variation of information will also judge them close.[1]
Definition
Suppose we have two partitions  and
and  of a set
of a set  into disjoint subsets,
namely
into disjoint subsets,
namely 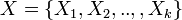 ,
, 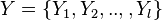 . Let
. Let 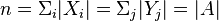 ,
, 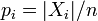 ,
, 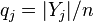 ,
, 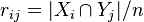 . Then the variation of information between the two partitions is:
. Then the variation of information between the two partitions is:
![VI(X; Y ) = - \sum_{i,j} r_{ij} \left[\log(r_{ij}/p_i)+\log(r_{ij}/q_j) \right]](../I/m/ae0475ae14199dca106d05b53b0929c0.png) .
.
This is equivalent to the shared information distance between the random variables i and j with respect to the uniform probability measure on  defined by
defined by 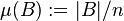 for
for 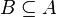 . The variation of information satisfies
. The variation of information satisfies
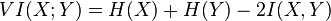 .
.
where 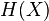 is the entropy of
is the entropy of  , and
, and 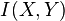 is mutual information between
is mutual information between  and
and  with respect to the uniform probability measure on
with respect to the uniform probability measure on  .
.
References
- ↑ Alexander Kraskov, Harald Stögbauer, Ralph G. Andrzejak, and Peter Grassberger, "Hierarchical Clustering Based on Mutual Information", (2003) ArXiv q-bio/0311039
Further reading
- Arabie, P.; Boorman, S. A. (1973). "Multidimensional scaling of measures of distance between partitions". Journal of Mathematical Psychology 10: 148–203. doi:10.1016/0022-2496(73)90012-6.
- Meila, Marina (2003). "Comparing Clusterings by the Variation of Information". Learning Theory and Kernel Machines: 173–187. doi:10.1007/978-3-540-45167-9_14.
- Meila, M. (2007). "Comparing clusterings—an information based distance". Journal of Multivariate Analysis 98 (5): 873–895. doi:10.1016/j.jmva.2006.11.013.
- Kingsford, Carl (2009). "Information Theory Notes" (PDF). Retrieved 22 September 2009.