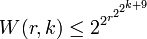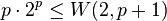Van der Waerden number

Van der Waerden's theorem states that for any positive integers r and k there exists a positive integer N such that if the integers {1, 2, ..., N} are colored, each with one of r different colors, then there are at least k integers in arithmetic progression all of the same color. The smallest such N is the van der Waerden number W(r,k).

Tables of Van der Waerden numbers

There are two cases in which the van der Waerden number is easy to compute: first, W(1,k)=k for any integer k, since one color produces only trivial colorings RRRRR...RRR (for the single color denoted R). Second, W(r,2)=r+1, since we may construct a coloring that avoids arithmetic progressions of length 2 by using each color at most once, but once we use a color twice, a length 2 arithmetic progression is formed (e.g., for r=3, the longest coloring we can get that avoids an arithmetic progression of length 2 is RGB). There are only a few other van der Waerden numbers that are known exactly. Bounds in this table taken from Rabung and Lotts[1] except where otherwise noted.

r\k 3 4 5 6 7 8
2 colors 9   35   178   1,132   > 3,703   > 11,495  
3 colors 27   293 [2]   > 2,173   > 11,191   > 48,811   > 238,400  
4 colors 76   > 1,048   > 17,705   > 91,331   > 420,217   > 2,388,317  
5 colors > 170   > 2,254   > 98,740   > 540,025   > 1,381,687   > 10,743,258  
6 colors > 223   > 9,778   > 98,748   > 816,981   > 7,465,909   > 57,445,718  

Van der Waerden numbers with r ≥ 2 are bounded above by

W(r,k)\le 2^{2^{r^{2^{2^{k+9}}}}}

as proved by Gowers.[3]

2-color van der Waerden numbers are bounded below by

p\cdot2^p\le W(2,p+1)

where p is prime, as proved by Berlekamp.[4]

One sometimes also writes w(r; k1, k2, ..., kr) to mean the smallest number w such that any coloring of the integers { 1, 2, ..., w } with r colors contains a progression of length ki of color i, for some i. Such numbers are called off-diagonal van der Waerden numbers. Thus W(r, k) = w(r; k, k, ..., k). Following is a list of some known van der Waerden numbers:

Known van der Waerden numbers
w(r;k1, k2, …, kr) Value Reference

w(2; 3,3)

9

Chvátal [5]

w(2; 3,4) 18 Chvátal [5]
w(2; 3,5) 22 Chvátal [5]
w(2; 3,6) 32 Chvátal [5]
w(2; 3,7) 46 Chvátal [5]
w(2; 3,8) 58 Beeler and O'Neil [6]
w(2; 3,9) 77 Beeler and O'Neil [6]
w(2; 3,10) 97 Beeler and O'Neil [6]
w(2; 3,11) 114 Landman, Robertson, and Culver [7]
w(2; 3,12) 135 Landman, Robertson, and Culver [7]
w(2; 3,13) 160 Landman, Robertson, and Culver [7]
w(2; 3,14) 186 Kouril [8]
w(2; 3,15) 218 Kouril [8]
w(2; 3,16) 238 Kouril [8]
w(2; 3,17) 279 Ahmed [9]
w(2; 3,18) 312 Ahmed [9]
w(2; 3,19) 349 Ahmed, Kullmann, and Snevily [10]
w(2; 4,4) 35 Chvátal [5]
w(2; 4,5) 55 Chvátal [5]
w(2; 4,6) 73 Beeler and O'Neil [6]
w(2; 4,7) 109 Beeler [11]
w(2; 4,8) 146 Kouril [8]
w(2; 4,9) 309 Ahmed [12]
w(2; 5,5) 178 Stevens and Shantaram [13]
w(2; 5,6) 206 Kouril [8]
w(2; 5,7) 260 Ahmed [14]
w(2; 6,6) 1132 Kouril and Paul [15]
w(3; 2, 3, 3) 14 Brown [16]
w(3; 2, 3, 4) 21 Brown [16]
w(3; 2, 3, 5) 32 Brown [16]
w(3; 2, 3, 6) 40 Brown [16]
w(3; 2, 3, 7) 55 Landman, Robertson, and Culver [7]
w(3; 2, 3, 8) 72 Kouril [8]
w(3; 2, 3, 9) 90 Ahmed [17]
w(3; 2, 3, 10) 108 Ahmed [17]
w(3; 2, 3, 11) 129 Ahmed [17]
w(3; 2, 3, 12) 150 Ahmed [17]
w(3; 2, 3, 13) 171 Ahmed [17]
w(3; 2, 3, 14) 202 Kouril [2]
w(3; 2, 4, 4) 40 Brown [16]
w(3; 2, 4, 5) 71 Brown [16]
w(3; 2, 4, 6) 83 Landman, Robertson, and Culver [7]
w(3; 2, 4, 7) 119 Kouril [8]
w(3; 2, 4, 8) 157 Kouril [2]
w(3; 2, 5, 5) 180 Ahmed [17]
w(3; 2, 5, 6) 246 Kouril [2]
w(3; 3, 3, 3) 27 Chvátal [5]
w(3; 3, 3, 4) 51 Beeler and O'Neil [6]
w(3; 3, 3, 5) 80 Landman, Robertson, and Culver [7]
w(3; 3, 3, 6) 107 Ahmed [12]
w(3; 3, 4, 4) 89 Landman, Robertson, and Culver [7]
w(3; 4, 4, 4) 293 Kouril [2]
w(4; 2, 2, 3, 3) 17 Brown [16]
w(4; 2, 2, 3, 4) 25 Brown [16]
w(4; 2, 2, 3, 5) 43 Brown [16]
w(4; 2, 2, 3, 6) 48 Landman, Robertson, and Culver [7]
w(4; 2, 2, 3, 7) 65 Landman, Robertson, and Culver [7]
w(4; 2, 2, 3, 8) 83 Ahmed [17]
w(4; 2, 2, 3, 9) 99 Ahmed [17]
w(4; 2, 2, 3, 10) 119 Ahmed [17]
w(4; 2, 2, 3, 11) 141 Schweitzer [18]
w(4; 2, 2, 4, 4) 53 Brown [16]
w(4; 2, 2, 4, 5) 75 Ahmed [17]
w(4; 2, 2, 4, 6) 93 Ahmed [17]
w(4; 2, 2, 4, 7) 143 Kouril [2]
w(4; 2, 3, 3, 3) 40 Brown [16]
w(4; 2, 3, 3, 4) 60 Landman, Robertson, and Culver [7]
w(4; 2, 3, 3, 5) 86 Ahmed [17]
w(4; 3, 3, 3, 3) 76 Beeler and O'Neil [6]
w(5; 2, 2, 2, 3, 3) 20 Landman, Robertson, and Culver [7]
w(5; 2, 2, 2, 3, 4) 29 Ahmed [17]
w(5; 2, 2, 2, 3, 5) 44 Ahmed [17]
w(5; 2, 2, 2, 3, 6) 56 Ahmed [17]
w(5; 2, 2, 2, 3, 7) 72 Ahmed [17]
w(5; 2, 2, 2, 3, 8) 88 Ahmed [17]
w(5; 2, 2, 2, 3, 9) 107 Kouril [2]
w(5; 2, 2, 2, 4, 4) 54 Ahmed [17]
w(5; 2, 2, 2, 4, 5) 79 Ahmed [17]
w(5; 2, 2, 2, 4, 6) 101 Kouril [2]
w(5; 2, 2, 3, 3, 3) 41 Landman, Robertson, and Culver [7]
w(5; 2, 2, 3, 3, 4) 63 Ahmed [17]
w(6; 2, 2, 2, 2, 3, 3) 21 Ahmed [17]
w(6; 2, 2, 2, 2, 3, 4) 33 Ahmed [17]
w(6; 2, 2, 2, 2, 3, 5) 50 Ahmed [17]
w(6; 2, 2, 2, 2, 3, 6) 60 Ahmed [17]
w(6; 2, 2, 2, 2, 4, 4) 56 Ahmed [17]
w(6; 2, 2, 2, 3, 3, 3) 42 Ahmed [17]
w(7; 2, 2, 2, 2, 2, 3, 3) 24 Ahmed [17]
w(7; 2, 2, 2, 2, 2, 3, 4) 36 Ahmed [17]
w(7; 2, 2, 2, 2, 2, 3, 5) 55 Ahmed [12]
w(7; 2, 2, 2, 2, 2, 3, 6) 65 Ahmed [14]
w(7; 2, 2, 2, 2, 2, 4, 4) 66 Ahmed [14]
w(7; 2, 2, 2, 2, 3, 3, 3) 45 Ahmed [14]
w(8; 2, 2, 2, 2, 2, 2, 3, 3) 25 Ahmed [17]
w(8; 2, 2, 2, 2, 2, 2, 3, 4) 40 Ahmed [12]
w(8; 2, 2, 2, 2, 2, 2, 3, 5) 61 Ahmed [14]
w(8; 2, 2, 2, 2, 2, 2, 3, 6) 71 Ahmed [14]
w(8; 2, 2, 2, 2, 2, 2, 4, 4) 67 Ahmed [14]
w(8; 2, 2, 2, 2, 2, 3, 3, 3) 49 Ahmed [14]
w(9; 2, 2, 2, 2, 2, 2, 2, 3, 3) 28 Ahmed [17]
w(9; 2, 2, 2, 2, 2, 2, 2, 3, 4) 42 Ahmed [14]
w(9; 2, 2, 2, 2, 2, 2, 2, 3, 5) 65 Ahmed [14]
w(9; 2, 2, 2, 2, 2, 2, 3, 3, 3) 52 Ahmed [14]
w(10; 2, 2, 2, 2, 2, 2, 2, 2, 3, 3) 31 Ahmed [14]
w(10; 2, 2, 2, 2, 2, 2, 2, 2, 3, 4) 45 Ahmed [14]
w(10; 2, 2, 2, 2, 2, 2, 2, 2, 3, 5) 70 Ahmed [14]
w(11; 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3) 33 Ahmed [14]
w(11; 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 4) 48 Ahmed [14]
w(12; 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3) 35 Ahmed [14]
w(12; 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 4) 52 Ahmed [14]
w(13; 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3) 37 Ahmed [14]
w(13; 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 4) 55 Ahmed [14]
w(14; 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3) 39 Ahmed [14]
w(15; 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3) 42 Ahmed [14]
w(16; 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3) 44 Ahmed [14]
w(17; 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3) 46 Ahmed [14]
w(18; 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3) 48 Ahmed [14]
w(19; 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3) 50 Ahmed [14]
w(20; 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3) 51 Ahmed [14]

Van der Waerden numbers are primitive recursive, as proved by Shelah;[19] in fact he proved that they are (at most) on the fifth level 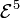\mathcal{E}^5 of the Grzegorczyk hierarchy.

See also

References

  1. ↑ John Rabung and Mark Lotts, http://www.combinatorics.org/ojs/index.php/eljc/article/view/v19i2p35/pdf
  2. ↑ 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 Kouril, Michal (2012). "Computing the van der Waerden number W(3,4)=293". Integers 12: A46.
  3. ↑ Gowers, W. T. (2001). "A new proof of Szemerédi's theorem". Geometric and Functional Analysis 11: 465–588. doi:10.1007/s00039-001-0332-9.
  4. ↑ Berlekamp, E. (1968). "A construction for partitions which avoid long arithmetic progressions". Canadian Mathematical Bulletin 11: 409–414. doi:10.4153/CMB-1968-047-7.
  5. ↑ 5.0 5.1 5.2 5.3 5.4 5.5 5.6 5.7 Chvátal, Vašek (1970). "Some unknown van der Waerden numbers". Combinatorial Structures and Their Applications (R.Guy et al.,eds.), New York.
  6. ↑ 6.0 6.1 6.2 6.3 6.4 6.5 Beeler, M.; O'Neil, P. (1979). "Some new van der Waerden numbers". Discrete Math. 28: 135–146. doi:10.1016/0012-365x(79)90090-6.
  7. ↑ 7.0 7.1 7.2 7.3 7.4 7.5 7.6 7.7 7.8 7.9 7.10 7.11 Landman, B.; Robertson, A.; Culver, C. (2005). "Some New Exact van der Waerden Numbers". Integers 5 (2): A10.
  8. ↑ 8.0 8.1 8.2 8.3 8.4 8.5 8.6 Kouril, Michal (2006). "A Backtracking Framework for Beowulf Clusters with an Extension to Multi-Cluster Computation and Sat Benchmark Problem Implementation". Ph. D. Thesis, University of Cincinnati, Engineering : Computer Science and Engineering.
  9. ↑ 9.0 9.1 Ahmed, Tanbir (2010). "Two new van der Waerden numbers w(2;3,17) and w(2;3,18)". Integers 10: 369–377, A32. doi:10.1515/integ.2010.032.
  10. ↑ Ahmed, Tanbir; Kullmann, Oliver; Snevily, Hunter. "On the van der Waerden numbers w(2;3,t)".
  11. ↑ Beeler, M. (1983). "A new van der Waerden number". Discrete Applied Math. 6: 207. doi:10.1016/0166-218x(83)90073-2.
  12. ↑ 12.0 12.1 12.2 12.3 Ahmed, Tanbir (2011). "On computation of exact van der Waerden numbers". Integers 11: A71.
  13. ↑ Stevens, R.; Shantaram, R. (1978). "Computer-generated van der Waerden partitions". Math. Computation 32: 635–636. doi:10.1090/s0025-5718-1978-0491468-x.
  14. ↑ 14.0 14.1 14.2 14.3 14.4 14.5 14.6 14.7 14.8 14.9 14.10 14.11 14.12 14.13 14.14 14.15 14.16 14.17 14.18 14.19 14.20 14.21 14.22 14.23 14.24 14.25 14.26 Ahmed, Tanbir (2013). "Some More Van der Waerden numbers". Journal of Integer Sequences 16: 13.4.4.
  15. ↑ Kouril, Michal; Paul, Jerome L. (2008). "The Van der Waerden Number W(2,6) is 1132". Experimental Mathematics 17 (1): 53–61. doi:10.1080/10586458.2008.10129025.
  16. ↑ 16.0 16.1 16.2 16.3 16.4 16.5 16.6 16.7 16.8 16.9 16.10 Brown, T. C. (1974). "Some new van der Waerden numbers (preliminary report)". Notices of the American Mathematical Society 21: A–432.
  17. ↑ 17.0 17.1 17.2 17.3 17.4 17.5 17.6 17.7 17.8 17.9 17.10 17.11 17.12 17.13 17.14 17.15 17.16 17.17 17.18 17.19 17.20 17.21 17.22 17.23 17.24 17.25 17.26 17.27 17.28 17.29 Ahmed, Tanbir (2009). "Some new van der Waerden numbers and some van der Waerden-type numbers". Integers 9: A6. doi:10.1515/integ.2009.007.
  18. ↑ Schweitzer, Pascal (2009). "Problems of Unknown Complexity, Graph isomorphism and Ramsey theoretic numbers". Ph. D. Thesis, U. des Saarlandes.
  19. ↑ Shelah, S. (1988). "Primitive Recursive Bounds for van der Waerden Numbers". Journal of the American Mathematical Society 1 (3): 683–697. JSTOR 1990952.

Further reading

External links