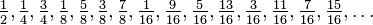Van der Corput sequence

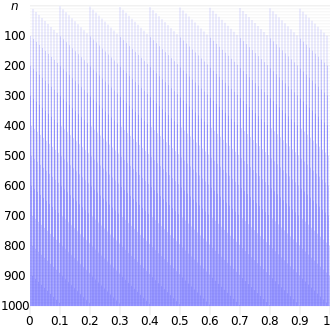
Illustration of the filling of the unit interval (horizontal axis) using the first n terms of the decimal Van der Corput sequence, for n from 0 to 999 (vertical axis)

A van der Corput sequence is the simplest one dimensional low-discrepancy sequence over the unit interval first published in 1935 by the Dutch mathematician J. G. van der Corput. It is constructed by reversing the base n representation of the sequence of natural numbers (1, 2, 3, …). For example, the decimal van der Corput sequence begins:

0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 0.01, 0.11, 0.21, 0.31, 0.41, 0.51, 0.61, 0.71, 0.81, 0.91, 0.02, 0.12, 0.22, 0.32, …

whereas the binary van der Corput sequence can be written as:

0.1₂, 0.01₂, 0.11₂, 0.001₂, 0.101₂, 0.011₂, 0.111₂, 0.0001₂, 0.1001₂, 0.0101₂, 0.1101₂, 0.0011₂, 0.1011₂, 0.0111₂, 0.1111₂, …

or, equivalently, as:

The elements of the van der Corput sequence (in any base) form a dense set in the unit interval: for any real number in [0, 1] there exists a subsequence of the van der Corput sequence that converges towards that number. They are also equidistributed over the unit interval.

See also

• Bit-reversal permutation
• Constructions of low-discrepancy sequences
• Halton sequence, a natural generalization of the van der Corput sequence to higher dimensions

References

• van der Corput, J.G. (1935), "Verteilungsfunktionen. I. Mitt.", Proc. Akad. Wet. Amsterdam (in German) 38: 813–821, Zbl 0012.34705 
• Kuipers, L.; Niederreiter, H. (2005) [1974], Uniform distribution of sequences, Dover Publications, p. 129,158, ISBN 0-486-45019-8, Zbl 0281.10001 

External links

• Van der Corput sequence at MathWorld