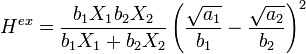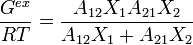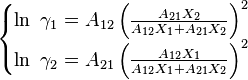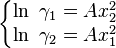Van Laar equation
The Van Laar equation is an activity model, which was developed by Johannes van Laar in 1910-1913, to describe phase equilibria of liquid mixtures. The equation was derived from the Van der Waals equation. The original van der Waals parameters didn't give good description of vapor-liquid phase equilibria, which forced the user to fit the parameters to experimental results. Because of this, the model lost the connection to molecular properties, and therefore it has to be regarded as an empirical model to correlate experimental results.
Equations
Van Laar derived the excess enthalpy from the van der Waals equation:[1]
In here ai and bi are the van der Waals parameters for attraction and excluded volume of component i. Since these parameters didn't lead to good phase equilibrium description the model was reduced to the form:
In here A12 and A21 are constants, which are obtained by regression of experimental vapor–liquid equilibrium data.
The activity coefficient of component i is derived by differentiation to xi. This yields:
This shows that the constants A12 and A21 are equal to logarithmic limiting activity coefficients 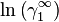 and
and 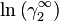 respectively. The model gives increasing (A12 and A21 >0) or only decreasing (A12 and A21 <0) activity coefficients with decreasing concentration. The model can not describe extrema in the activity coefficient along the concentration range.
respectively. The model gives increasing (A12 and A21 >0) or only decreasing (A12 and A21 <0) activity coefficients with decreasing concentration. The model can not describe extrema in the activity coefficient along the concentration range.
In case 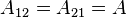 , which implies that the molecules are of equal size but different in polarity, then the equations become:
, which implies that the molecules are of equal size but different in polarity, then the equations become:
In this case the activity coefficients mirror at x1=0.5. When A=0 the model the activity coefficients are unity, thus describing an ideal mixture.
References
- ↑ The Open Thermodynamics Journal, 2010, 4, 129-140