VList

Not to be confused with Vlist, a municipality in the Netherlands.

In computer science, the VList is a persistent data structure designed by Phil Bagwell in 2002 that combines the fast indexing of arrays with the easy extension of cons-based (or singly linked) linked lists.^[1]

Like arrays, VLists have constant-time lookup on average and are highly compact, requiring only O(log n) storage for pointers, allowing them to take advantage of locality of reference. Like singly linked or cons-based lists, they are persistent, and elements can be added to or removed from the front in constant time. Length can also be found in O(log n) time.

Operations

The primary operations of a VList are:

Locate the kth element (O(1) average, O(log n) worst-case)
Add an element to the front of the VList (O(1) average, with an occasional allocation)
Obtain a new array beginning at the second element of an old array (O(1))
Compute the length of the list (O(log n))

Advantages and Disadvantages

The primary advantage VLists have over arrays is that different updated versions of the VList automatically share structure. Because VLists are immutable, they are most useful in functional programming languages, where their efficiency allows a purely functional implementation of data structures traditionally thought to require mutable arrays, such as hash tables.

However, VLists also have a number of disadvantages over their competitors:

While immutability is a benefit, it is also a drawback, making it inefficient to modify elements in the middle of the array.
Access near the end of the list can be as expensive as O(log n); it is only constant on average over all elements. This is still, however, much better than performing the same operation on cons-based lists.
Wasted space in the first block is proportional to n. This is similar to linked lists, but there are data structures with less overhead. When used as a fully persistent data structure, the overhead may be considerably higher and this data structure may not be appropriate.

Structure

The underlying structure of a VList can be seen as a singly linked list of arrays whose sizes decrease geometrically; in its simplest form, the first contains the first half of the elements in the list, the next the first half of the remainder, and so on. Each of these blocks stores some information such as its size and a pointer to the next.

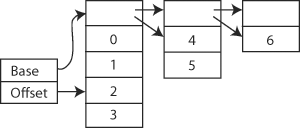
An array-list. The reference shown refers to the VList (2,3,4,5,6).

The average constant-time indexing operation comes directly from this structure; given a random valid index, we simply observe the size of the blocks and follow pointers until we reach the one it should be in. The chance is 1/2 that it falls in the first block and we need not follow any pointers; the chance is 1/4 we have to follow only one, and so on, so that the expected number of pointers we have to follow is:

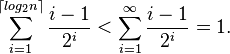
$\sum_{i=1}^{\lceil log_2 n \rceil} \frac{i-1}{2^i} < \sum_{i=1}^{\infty} \frac{i-1}{2^i} = 1.$

Any particular reference to a VList is actually a <base, offset> pair indicating the position of its first element in the data structure described above. The base part indicates which of the arrays its first element falls in, while the offset part indicates its index in that array. This makes it easy to "remove" an element from the front of the list; we simply increase the offset, or increase the base and set the offset to zero if the offset goes out of range. If a particular reference is the last to leave a block, the block will be garbage-collected if such facilities are available, or otherwise must be freed explicitly.

Because the lists are constructed incrementally, the first array in the array list may not contain twice as many values as the next one, although the rest do; this does not significantly impact indexing performance. We nevertheless allocate this much space for the first array, so that if we add more elements to the front of the list in the future we can simply add them to this list and update the size. If the array fills up, we create a new array, twice as large again as this one, and link it to the old first array.

The trickier case, however, is adding a new item to the front of a list, call it A, which starts somewhere in the middle of the array-list data structure. This is the operation that allows VLists to be persistent. To accomplish this, we create a new array, and we link it to the array containing the first element of A. The new array must also store the offset of the first element of A in that array. Then, we can proceed to add any number of items we like to our new array, and any references into this new array will point to VLists which share a tail of values with the old array. Note that with this operation it is possible to create VLists which degenerate into simple linked lists, thus obliterating the performance claims made at the beginning of this article.

Variants

VList may be modified to support the implementation of a growable array. In the application of a growable array, immutability is no longer required. Instead of growing at the beginning of the list, the ordering interpretation is reversed to allow growing at the end of the array.

References

↑ Bagwell, Phil (2002), Fast Functional Lists, Hash-Lists, Deques and Variable Length Arrays, EPFL