Universal point set
In graph drawing, a universal point set of order n is a set S of points in the Euclidean plane with the property that every n-vertex planar graph has a straight-line drawing in which the vertices are all placed at points of S.
Bounds on the size of universal point sets

When n is ten or less, there exist universal point sets with exactly n points, but for all n ≥ 15 additional points are required.[1]
Several authors have shown that subsets of the integer lattice of size O(n) × O(n) are universal. In particular, de Fraysseix, Pach & Pollack (1988) showed that a grid of (2n − 3) × (n − 1) points is universal, and Schnyder (1990) reduced this to a triangular subset of an (n − 1) × (n − 1) grid, with n2/2 − O(n) points. By modifying the method of de Fraysseix et al., Brandenburg (2008) found an embedding of any planar graph into a triangular subset of the grid consisting of 4n2/9 points. A universal point set in the form of a rectangular grid must have size at least n/3 × n/3[2] but this does not rule out the possibility of smaller universal point sets of other types. The smallest known universal point sets are not based on grids, but are instead constructed from superpatterns (permutations that contain all permutation patterns of a given size); the universal point sets constructed in this way have size n2/4 − O(n).[3]
de Fraysseix, Pach & Pollack (1988) proved the first nontrivial lower bound on the size of a universal point set, with a bound of the form n + Ω(√n), and Chrobak & Karloff (1989) showed that universal point sets must contain at least 1.098n − o(n) points. Kurowski (2004) stated an even stronger bound of 1.235n − o(n), which remains the best lower bound known.[4]
Closing the gap between the known linear lower bounds and quadratic upper bounds remains an open problem.[5]
Special classes of graphs
Subclasses of the planar graphs may, in general, have smaller universal sets (sets of points that allow straight-line drawings of all n-vertex graphs in the subclass) than the full class of planar graphs, and in many cases universal point sets of exactly n points are possible. For instance, it is not hard to see that every set of n points in convex position (forming the vertices of a convex polygon) is universal for the n-vertex outerplanar graphs, and in particular for trees. Less obviously, every set of n points in general position (no three collinear) remains universal for outerplanar graphs.[6]
Planar graphs that can be partitioned into nested cycles, and planar graphs of bounded pathwidth, have universal point sets of nearly-linear size.[7] Planar 3-trees have universal point sets of size O(n5/3); the same bound also applies to series-parallel graphs.[8]
Other drawing styles
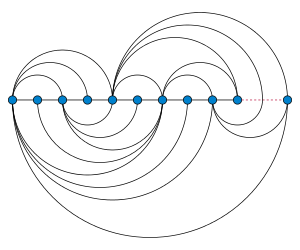
As well as for straight-line graph drawing, universal point sets have been studied for other drawing styles; in many of these cases, universal point sets with exactly n points exist, based on a topological book embedding in which the vertices are placed along a line in the plane and the edges are drawn as curves that cross this line at most once. For instance, every set of n collinear points is universal for an arc diagram in which each edge is represented as either a single semicircle or a smooth curve formed from two semicircles.[9]
By using a similar layout, every convex curve in the plane can be shown to contain an n-point subset that is universal for polyline drawing with at most one bend per edge.[10] This set contains only the vertices of the drawing, not the bends; larger sets are known that can be used for polyline drawing with all vertices and all bends placed within the set.[11]
Notes
- ↑ Cardinal, Hoffmann & Kusters (2012).
- ↑ Dolev, Leighton & Trickey (1984); Chrobak & Karloff (1989); Demaine & O'Rourke (2002–2012). A weaker quadratic lower bound on the grid size needed for planar graph drawing was given earlier by Valiant (1981).
- ↑ Bannister et al. (2013).
- ↑ Mondal (2012) claimed that Kurowski's proof was erroneous, but later (after discussion with Jean Cardinal) retracted this claim; see Explanation Supporting Kurowski's Proof, D. Mondal, updated August 9, 2013.
- ↑ Demaine & O'Rourke (2002–2012); Brandenburg et al. (2003); Mohar (2007).
- ↑ Gritzmann et al. (1991).
- ↑ Angelini et al. (2012); Bannister et al. (2013).
- ↑ Fulek & Toth (2013)
- ↑ Giordano et al. (2007).
- ↑ Everett et al. (2010).
- ↑ Dujmović et al. (2013).
References
- Angelini, Patrizio; Di Battista, Giuseppe; Kaufmann, Michael; Mchedlidze, Tamara; Roselli, Vincenzo; Squarcella, Claudio (2012), "Small point sets for simply-nested planar graphs", in van Kreveld, Marc; Speckmann, Bettina, Graph Drawing: 19th International Symposium, GD 2011, Eindhoven, The Netherlands, September 21–23, 2011, Revised Selected Papers, LNCS 7034, Berlin, Heidelberg: Springer-Verlag, pp. 75–85, doi:10.1007/978-3-642-25878-7_8.
- Bannister, Michael J.; Cheng, Zhanpeng; Devanny, William E.; Eppstein, David (2013), "Superpatterns and universal point sets", Proc. 21st International Symposium on Graph Drawing (GD 2013), arXiv:1308.0403.
- Brandenburg, Franz J. (2008), "Drawing planar graphs on
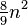 area", The International Conference on Topological and Geometric Graph Theory, Electronic Notes in Discrete Mathematics 31, Elsevier, pp. 37–40, doi:10.1016/j.endm.2008.06.005, MR 2571101.
area", The International Conference on Topological and Geometric Graph Theory, Electronic Notes in Discrete Mathematics 31, Elsevier, pp. 37–40, doi:10.1016/j.endm.2008.06.005, MR 2571101. - Brandenburg, Franz-Josef; Eppstein, David; Goodrich, Michael T.; Kobourov, Stephen G.; Liotta, Giuseppe; Mutzel, Petra (2003), "Selected open problems in graph drawing", in Liotta, Giuseppe, Graph Drawing: 11th International Symposium, GD 2003, Perugia, Italy, September 21–24, 2003 Revised Papers, Lecture Notes in Computer Science 2912, Springer-Verlag, pp. 515–539, doi:10.1007/978-3-540-24595-7_55. See in particular problem 11 on p. 520.
- Cardinal, Jean; Hoffmann, Michael; Kusters, Vincent (2012), On Universal Point Sets for Planar Graphs, arXiv:1209.3594.
- Chrobak, M.; Karloff, H. (1989), "A lower bound on the size of universal sets for planar graphs", SIGACT News 20: 83–86, doi:10.1145/74074.74088.
- de Fraysseix, Hubert; Pach, János; Pollack, Richard (1988), "Small sets supporting Fary embeddings of planar graphs", Twentieth Annual ACM Symposium on Theory of Computing, pp. 426–433, doi:10.1145/62212.62254, ISBN 0-89791-264-0.
- Demaine, E.; O'Rourke, J. (2002–2012), "Problem 45: Smallest Universal Set of Points for Planar Graphs", The Open Problems Project, retrieved 2013-03-19.
- Dolev, Danny; Leighton, Tom; Trickey, Howard (1984), "Planar embedding of planar graphs", Advances in Computing Research 2: 147–161.
- Dujmović, V.; Evans, W. S.; Lazard, S.; Lenhart, W.; Liotta, G.; Rappaport, D.; Wismath, S. K. (2013), "On point-sets that support planar graphs", Comput. Geom. Theory Appl. 46 (1): 29–50.
- Everett, Hazel; Lazard, Sylvain; Liotta, Giuseppe; Wismath, Stephen (2010), "Universal Sets of n Points for One-Bend Drawings of Planar Graphs with n Vertices", Discrete and Computational Geometry 43 (2): 272–288, doi:10.1007/s00454-009-9149-3.
- Fulek, Radoslav; Toth, Csaba (2013), "Universal point sets for planar three-trees", Algorithms & Data Structures Symposium (WADS), to appear, arXiv:1212.6148.
- Giordano, Francesco; Liotta, Giuseppe; Mchedlidze, Tamara; Symvonis, Antonios (2007), "Computing upward topological book embeddings of upward planar digraphs", Algorithms and Computation: 18th International Symposium, ISAAC 2007, Sendai, Japan, December 17-19, 2007, Proceedings, Lecture Notes in Computer Science 4835, Springer, pp. 172–183, doi:10.1007/978-3-540-77120-3_17.
- Gritzmann, P.; Mohar, B.; Pach, János; Pollack, Richard (1991), "Embedding a planar triangulation with vertices at specified positions", American Mathematical Monthly 98 (2): 165–166, JSTOR 2323956
.
- Kurowski, Maciej (2004), "A 1.235 lower bound on the number of points needed to draw all n-vertex planar graphs", Information Processing Letters 92 (2): 95–98, doi:10.1016/j.ipl.2004.06.009, MR 2085707.
- Mohar, Bojan (2007), "Universal point sets for planar graphs", Open Problem Garden, retrieved 2013-03-20.
- Mondal, Debajyoti (2012), Embedding a Planar Graph on a Given Point Set, Masters thesis, Department of Computer Science, University of Manitoba.
- Schnyder, Walter (1990), "Embedding planar graphs on the grid", Proc. 1st ACM/SIAM Symposium on Discrete Algorithms (SODA), pp. 138–148.
- Valiant, L. G. (1981), "Universality considerations in VLSI circuits", IEEE Transactions on Computers C–30 (2): 135–140, doi:10.1109/TC.1981.6312176