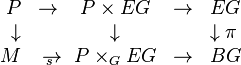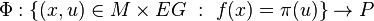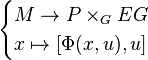Universal bundle

In mathematics, the universal bundle in the theory of fiber bundles with structure group a given topological group $G$ , is a specific bundle over a classifying space $BG$ , such that every bundle with the given structure group $G$ over $M$ is a pullback by means of a continuous map $M \to BG$ .

Existence of a universal bundle

In the CW complex category

When the definition of the classifying space takes place within the homotopy category of CW complexes, existence theorems for universal bundles arise from Brown's representability theorem.

For compact Lie groups

We will first prove:

Proposition. Let

G

be a compact Lie group. There exists a contractible space

EG

on which

G

acts freely. The projection

EG \to BG

is a

G

-principal fibre bundle.

Proof. There exists an injection of $G$ into a unitary group $U (n)$ for $n$ big enough.^[1] If we find $EU (n)$ then we can take $EG$ to be $EU (n)$ . The construction of $EU (n)$ is given in classifying space for $U (n)$ .

The following Theorem is a corollary of the above Proposition.

Theorem. If

M

is a paracompact manifold and

P \to M

is a principal

G

-bundle, then there exists a map

f : M \to BG

, unique up to homotopy, such that

P

is isomorphic to

f * (EG)

, the pull-back of the

G

-bundle

EG \to BG

f

Proof. On one hand, the pull-back of the bundle $π : EG \to BG$ by the natural projection $P \times G EG \to BG$ is the bundle $P \times EG$ . On the other hand, the pull-back of the principal $G$ -bundle $P \to M$ by the projection $p : P \times G EG \to M$ is also $P \times EG$

\begin{array}{rcccl} P & \to & P\times EG & \to & EG \\ \downarrow & & \downarrow & & \downarrow \pi \\ M & \to_{\!\!\!\!\!\!\!s} & P\times_G EG & \to & BG \end{array}

Since $p$ is a fibration with contractible fibre $EG$ , sections of $p$ exist.^[2] To such a section $s$ we associate the composition with the projection $P \times G EG \to BG$ . The map we get is the $f$ we were looking for.

For the uniqueness up to homotopy, notice that there exists a one to one correspondence between maps $f : M \to BG$ such that $f * (EG) \to M$ is isomorphic to $P \to M$ and sections of $p$ . We have just seen how to associate a $f$ to a section. Inversely, assume that $f$ is given. Let $Φ : f * (EG) \to P$ be an isomorphism:

\Phi: \left \{ (x,u) \in M \times EG \ : \ f(x)=\pi(u) \right \} \to P

Now, simply define a section by

\begin{cases} M \to P\times_G EG \\ x \mapsto \lbrack \Phi(x,u),u \rbrack \end{cases}

Because all sections of $p$ are homotopic, the homotopy class of $f$ is unique.

Use in the study of group actions

The total space of a universal bundle is usually written $EG$ . These spaces are of interest in their own right, despite typically being contractible. For example in defining the homotopy quotient or homotopy orbit space of a group action of $G$ , in cases where the orbit space is pathological (in the sense of being a non-Hausdorff space, for example). The idea, if $G$ acts on the space $X$ , is to consider instead the action on $Y = X \times EG$ , and corresponding quotient. See equivariant cohomology for more detailed discussion.

If $EG$ is contractible then $X$ and $Y$ are homotopy equivalent spaces. But the diagonal action on $Y$ , i.e. where $G$ acts on both $X$ and $EG$ coordinates, may be well-behaved when the action on $X$ is not.

Examples

Classifying space for U(n)

External links

PlanetMath page of universal bundle examples

Notes

↑ J. J. Duistermaat and J. A. Kolk,-- Lie Groups, Universitext, Springer. Corollary 4.6.5
↑ A.~Dold -- Partitions of Unity in the Theory of Fibrations,Annals of Math., vol. 78, No 2 (1963)