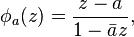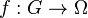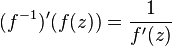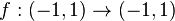Univalent function
In mathematics, in the branch of complex analysis, a holomorphic function on an open subset of the complex plane is called univalent if it is injective.
Examples
Any mapping 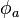 of the open unit disc to itself. The function
of the open unit disc to itself. The function
where 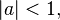 is univalent.
is univalent.
Basic properties
One can prove that if  and
and 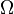 are two open connected sets in the complex plane, and
are two open connected sets in the complex plane, and
is a univalent function such that 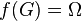 (that is,
(that is,  is surjective), then the derivative of
is surjective), then the derivative of  is never zero,
is never zero,  is invertible, and its inverse
is invertible, and its inverse 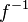 is also holomorphic. More, one has by the chain rule
is also holomorphic. More, one has by the chain rule
for all 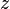 in
in 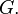
Comparison with real functions
For real analytic functions, unlike for complex analytic (that is, holomorphic) functions, these statements fail to hold. For example, consider the function
given by ƒ(x) = x3. This function is clearly injective, but its derivative is 0 at x = 0, and its inverse is not analytic, or even differentiable, on the whole interval (−1, 1). Consequently, if we enlarge the domain to an open subset G of the complex plane, it must fail to be injective; and this is the case, since (for example) f(εω) = f(ε) (where ω is a primitive cube root of unity and ε is a positive real number smaller than the radius of G as a neighbourhood of 0).
References
- John B. Conway. Functions of One Complex Variable I. Springer-Verlag, New York, 1978. ISBN 0-387-90328-3.
- John B. Conway. Functions of One Complex Variable II. Springer-Verlag, New York, 1996. ISBN 0-387-94460-5.
This article incorporates material from univalent analytic function on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.