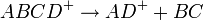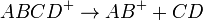Unimolecular ion decomposition

Unimolecular ion decomposition is the fragmentation of a gas phase ion in a reaction with a molecularity of one.[1] Ions with sufficient internal energy may fragment in a mass spectrometer, which in some cases may degrade the mass spectrometer performance, but in other cases, such as tandem mass spectrometry, the fragmentation can reveal information about the structure of the ion.

Wahrhaftig diagram

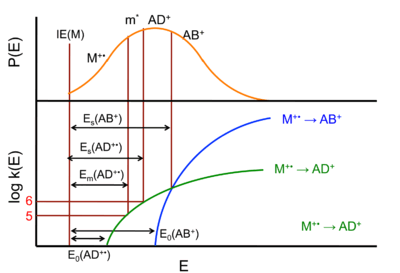
Wahrhaftig diagram showing the relationship between internal energy and unimolecular ion decomposition for a hypothetical ion ABCD+.

A Wahrhaftig diagram (named after Austin L. Wahrhaftig) illustrates the relative contributions in unimolecular ion decomposition of direct fragmentation and fragmentation following rearrangement. The x-axis of the digram represents the internal energy of the ion. The lower part of the diagram shows the logarithm of the rate constant k for unimolecular dissociation whereas the upper portion of the diagram indicates the probability of forming a particular product ion. The green trace in the lower part of the diagram indicates the rate of the rearrangement reacton given by

ABCD^+ \to AD^+ + BC\,

and the blue trace indicates the direct cleavage reaction

ABCD^+ \to AB^+ + CD\,

A rate constant of 106 s−1 is sufficiently fast for ion decomposition within the ion source of a typical mass spectrometer. Ions with rate constants less than 106 s−1 and greater than approximately 105 s−1 (lifetimes between 10-5 and 10-6 s) have a high probability of decomposing in the mass spectrometer between the ion source and the detector. These rate constants are indicated in the Wahrhaftig diagram by the log k = 5 and log k = 6 dashed lines.

Indicated on the rate constant plot are the reaction critical energy (also called the activation energy) for the formation of AD+, E0(AD+) and AB+, E0(AB+). These represent the minimum internal energy of ABCD+ required to form the respective product ions: the difference in the zero point energy of ABCD+ and that of the activated complex.

When the internal energy of ABCD+ is greater than Em(AD+), the ions are metastable (indicated by m*); this occurs near log k > 5. A metastable ion has sufficient internal energy to dissociate prior to detection.[2][3] The energy Es(AD+) is defined as the internal energy of ABCD+ that results in an equal probability that ABCD+and AD+ leave the ion source, which occurs at near log k = 6. When the precursor ion has an internal energy equal to Es(AB+), the rates of formation of AD+ and AB+ are equal.

Thermodynamic and kinetic effects

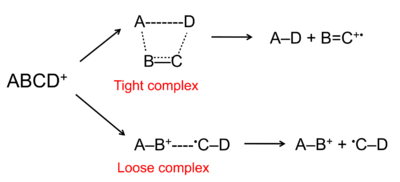
Schematic of "tight" and "loose" transition state complexes for a hypothetical ion ABCD+.

Like all chemical reactions, the unimolecular decomposition of ions is subject to thermodynamic versus kinetic reaction control: the kinetic product forms faster, whereas the thermodynamic product is more stable.[4] In the decomposition of ABCD+, the reaction to form AD+ is thermodynamically favored and the reaction to form AB+is kinetically favored. This is because the AD+ reaction has favorable enthalpy and the AB+ has favorable entropy.

In the reaction depicted schematically in the figure, the rearrangement reaction forms a double bond B=C and a new single bond A-D, which offsets the cleavage of the A-B and C-D bonds. The formation of AB+ requires bond cleavage without the offsetting bond formation. However, the steric effect makes it more difficult for the molecule to achieve the rearrangement transition state and form AD+. The activated complex with strict steric requirements is referred to as a "tight complex" whereas the transition state without such requirements is called a "loose complex."

See also

References

  1. ↑ Brenton, A G; Morgan, R P; Beynon, J H (1979). "Unimolecular Ion Decomposition". Annual Review of Physical Chemistry 30: 51. Bibcode:1979ARPC...30...51B. doi:10.1146/annurev.pc.30.100179.000411.
  2. ↑ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version:  (2006–) "metastable ion (in mass spectrometry)".
  3. ↑ Hipple, J.; Condon, E. (1945). "Detection of Metastable Ions with the Mass Spectrometer". Physical Review 68: 54. Bibcode:1945PhRv...68...54H. doi:10.1103/PhysRev.68.54.
  4. ↑ Tureček, František; McLafferty, Fred W. (1993). Interpretation of mass spectra. Sausalito, Calif: University Science Books. p. 115. ISBN 0-935702-25-3.