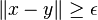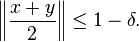Uniformly convex space
In mathematics, uniformly convex spaces (or uniformly rotund spaces) are common examples of reflexive Banach spaces. The concept of uniform convexity was first introduced by James A. Clarkson in 1936.
Definition
A uniformly convex space is a normed vector space so that, for every 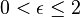 there is some
there is some 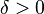 so that for any two vectors with
so that for any two vectors with 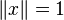 and
and  the condition
the condition
implies that:
Intuitively, the center of a line segment inside the unit ball must lie deep inside the unit ball unless the segment is short.
Properties
- The Milman–Pettis theorem states that every uniformly convex Banach space is reflexive, while the converse is not true.
- If
 is a sequence in a uniformly convex Banach space which converges weakly to
is a sequence in a uniformly convex Banach space which converges weakly to  and satisfies
and satisfies  then
then 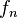 converges strongly to
converges strongly to  , that is,
, that is, 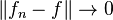 .
. - A Banach space
 is uniformly convex if and only if its dual
is uniformly convex if and only if its dual 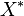 is uniformly smooth.
is uniformly smooth. - Every uniformly convex space is strictly convex.
Examples
- Every Hilbert space is uniformly convex.
- Every closed subspace of a uniformly convex Banach space is uniformly convex.
- Hanner's inequalities imply that Lp spaces
 are uniformly convex.
are uniformly convex. - Conversely,
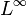 is not uniformly convex. For example, in
is not uniformly convex. For example, in 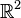 consider
consider  and
and 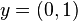 . Then
. Then  and
and 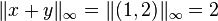 , but
, but 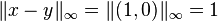 .
.
See also
References
- Clarkson, J. A. (1936). "Uniformly convex spaces". Trans. Amer. Math. Soc. (American Mathematical Society) 40 (3): 396–414. doi:10.2307/1989630. JSTOR 1989630..
- Hanner, O. (1956). "On the uniform convexity of
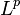 and
and 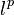 ". Ark. Mat. 3: 239–244. doi:10.1007/BF02589410..
". Ark. Mat. 3: 239–244. doi:10.1007/BF02589410..
- Beauzamy, Bernard (1985) [1982]. Introduction to Banach Spaces and their Geometry (Second revised ed.). North-Holland. ISBN 0-444-86416-4.
- Per Enflo (1972). "Banach spaces which can be given an equivalent uniformly convex norm". Israel Journal of Mathematics 13 (3–4): 281–288. doi:10.1007/BF02762802.
- Lindenstrauss, Joram and Benyamini, Yoav. Geometric nonlinear functional analysis Colloquium publications, 48. American Mathematical Society.