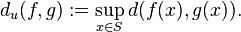Uniformly Cauchy sequence
In mathematics, a sequence of functions 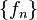 from a set S to a metric space M is said to be uniformly Cauchy if:
from a set S to a metric space M is said to be uniformly Cauchy if:
- For all
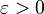 , there exists
, there exists 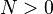 such that for all
such that for all 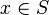 :
: 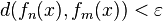 whenever
whenever 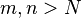 .
.
Another way of saying this is that 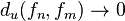 as
as 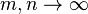 , where the uniform distance
, where the uniform distance 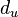 between two functions is defined by
between two functions is defined by
Convergence criteria
A sequence of functions {fn} from S to M is pointwise Cauchy if, for each x ∈ S, the sequence {fn(x)} is a Cauchy sequence in M. This is a weaker condition than being uniformly Cauchy. Nevertheless, if the metric space M is complete, then any pointwise Cauchy sequence converges pointwise to a function from S to M. Similarly, any uniformly Cauchy sequence will tend uniformly to such a function.
The uniform Cauchy property is frequently used when the S is not just a set, but a topological space, and M is a complete metric space. The following theorem holds:
- Let S be a topological space and M a complete metric space. Then any uniformly Cauchy sequence of continuous functions fn : S → M tends uniformly to a unique continuous function f : S → M.
Generalization to uniform spaces
A sequence of functions 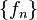 from a set S to a metric space U is said to be uniformly Cauchy if:
from a set S to a metric space U is said to be uniformly Cauchy if:
- For all
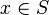 and for any entourage
and for any entourage  , there exists
, there exists 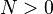 such that
such that 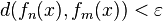 whenever
whenever 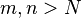 .
.