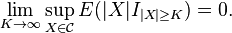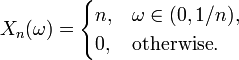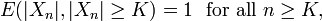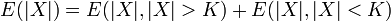Uniform integrability
Uniform integrability is an important concept in real analysis, functional analysis and measure theory, and plays a vital role in the theory of martingales.
Definition
Let 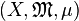 be a positive measure space. A set
be a positive measure space. A set 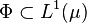 is called uniformly integrable if to each
is called uniformly integrable if to each 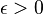 there corresponds a
there corresponds a 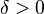 such that
such that
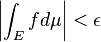
whenever 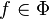 and
and 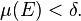
Formal definition
The following definition applies.[1]
- A class
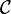 of random variables is called uniformly integrable (UI) if given
of random variables is called uniformly integrable (UI) if given 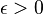 , there exists
, there exists 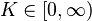 such that
such that 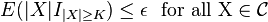 , where
, where 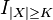 is the indicator function
is the indicator function 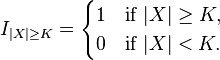 .
.
- An alternative definition involving two clauses may be presented as follows: A class
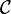 of random variables is called uniformly integrable if:
of random variables is called uniformly integrable if:
- There exists a finite
 such that, for every
such that, for every  in
in 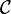 ,
, 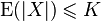 .
. - For every
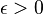 there exists
there exists 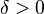 such that, for every measurable
such that, for every measurable  such that
such that 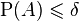 and every
and every  in
in 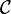 ,
, 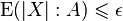 .
.
- There exists a finite
Related corollaries
The following results apply.
- Definition 1 could be rewritten by taking the limits as
- A non-UI sequence. Let
![\Omega = [0,1] \subset \mathbb{R}](../I/m/2f64868c72e1cb9ae59af6ef1ae48a75.png) , and define
, and define
- Clearly
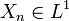 , and indeed
, and indeed 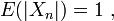 for all n. However,
for all n. However,
- and comparing with definition 1, it is seen that the sequence is not uniformly integrable.
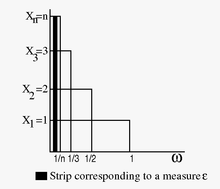
Non-UI sequence of RVs. The area under the strip is always equal to 1, but 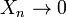 pointwise.
pointwise.
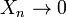 pointwise.
pointwise.- By using Definition 2 in the above example, it can be seen that the first clause is satisfied as
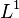 norm of all
norm of all 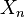 s are 1 i.e., bounded. But the second clause does not hold as given any
s are 1 i.e., bounded. But the second clause does not hold as given any 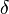 positive, there is an interval
positive, there is an interval 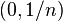 with measure less than
with measure less than 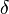 and
and ![E[|X_m|: (0, 1/n)] =1](../I/m/8fbc0f7b8774cf37c85ef236a6754176.png) for all
for all 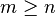 .
. - If
 is a UI random variable, by splitting
is a UI random variable, by splitting
- and bounding each of the two, it can be seen that a uniformly integrable random variable is always bounded in
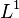 .
.
- If any sequence of random variables
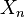 is dominated by an integrable, non-negative
is dominated by an integrable, non-negative  : that is, for all ω and n,
: that is, for all ω and n,
- then the class
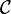 of random variables
of random variables 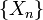 is uniformly integrable.
is uniformly integrable.
- A class of random variables bounded in
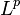 (
(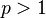 ) is uniformly integrable.
) is uniformly integrable.
Relevant theorems
- A class of random variables
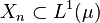 is uniformly integrable if and only if it is relatively compact for the weak topology
is uniformly integrable if and only if it is relatively compact for the weak topology 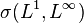 .
.
- de la Vallée-Poussin theorem[3]
- The family
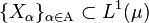 is uniformly integrable if and only if there exists a non-negative increasing convex function
is uniformly integrable if and only if there exists a non-negative increasing convex function 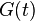 such that
such that
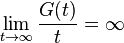 and
and 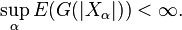
Relation to convergence of random variables
Main article: convergence of random variables
- A sequence
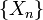 converges to
converges to  in the
in the 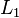 norm if and only if it converges in measure to
norm if and only if it converges in measure to  and it is uniformly integrable. In probability terms, a sequence of random variables converging in probability also converge in the mean if and only if they are uniformly integrable.[4] This is a generalization of the dominated convergence theorem.
and it is uniformly integrable. In probability terms, a sequence of random variables converging in probability also converge in the mean if and only if they are uniformly integrable.[4] This is a generalization of the dominated convergence theorem.
Citations
- ↑ Williams, David (1997). Probability with Martingales (Repr. ed.). Cambridge: Cambridge Univ. Press. pp. 126–132. ISBN 978-0-521-40605-5.
- ↑ Dellacherie, C. and Meyer, P.A. (1978). Probabilities and Potential, North-Holland Pub. Co, N. Y. (Chapter II, Theorem T25).
- ↑ Meyer, P.A. (1966). Probability and Potentials, Blaisdell Publishing Co, N. Y. (p.19, Theorem T22).
- ↑ Bogachev, Vladimir I. (2007). Measure Theory Volume I. Berlin Heidelberg: Springer-Verlag. p. 268. doi:10.1007/978-3-540-34514-5_4. ISBN 3-540-34513-2.
References
- A.N. Shiryaev (1995). Probability (2 ed.). New York: Springer-Verlag. pp. 187–188. ISBN 978-0-387-94549-1.
- Walter Rudin (1987). Real and Complex Analysis (3 ed.). Singapore: McGraw–Hill Book Co. p. 133. ISBN 0-07-054234-1.
- J. Diestel and J. Uhl (1977). Vector measures, Mathematical Surveys 15, American Mathematical Society, Providence, RI ISBN 978-0-8218-1515-1