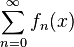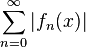Uniform absolute-convergence

In mathematics, uniform absolute-convergence is a type of convergence for series of functions. Like absolute-convergence, it has the useful property that it is preserved when the order of summation is changed.

Motivation

A convergent series of numbers can often be reordered in such a way that the new series diverges. This is not possible for series of nonnegative numbers, however, so the notion of absolute-convergence precludes this phenomenon. When dealing with uniformly convergent series of functions, the same phenomenon occurs: the series can potentially be reordered into a non-uniformly convergent series, or a series which does not even converge pointwise. This is impossible for series of nonnegative functions, so the notion of uniform absolute-convergence can be used to rule out these possibilities.

Definition

Given a set X and functions 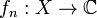$f_n : X \to \mathbb{C}$ (or to any normed vector space), the series

\sum_{n=0}^{\infty} f_n(x)

is called uniformly absolutely-convergent if the series of nonnegative functions

\sum_{n=0}^{\infty} |f_n(x)|

is uniformly convergent.^[1]

Distinctions

A series can be uniformly convergent and absolutely convergent without being uniformly absolutely-convergent. For example, if ƒ_n(x) = xⁿ/n on the open interval (−1,0), then the series Σf_n(x) converges uniformly by comparison of the partial sums to those of Σ(−1)ⁿ/n, and the series Σ|f_n(x)| converges absolutely at each point by the geometric series test, but Σ|f_n(x)| does not converge uniformly. Intuitively, this is because the absolute-convergence gets slower and slower as x approaches −1, where convergence holds but absolute convergence fails.

Generalizations

If a series of functions is uniformly absolutely-convergent on some neighborhood of each point of a topological space, it is locally uniformly absolutely-convergent. If a series is uniformly absolutely-convergent on all compact subsets of a topological space, it is compactly (uniformly) absolutely-convergent. If the topological space is locally compact, these notions are equivalent.

Properties

If a series of functions into C (or any Banach space) is uniformly absolutely-convergent, then it is uniformly convergent.
Uniform absolute-convergence is independent of the ordering of a series. This is because, for a series of nonnegative functions, uniform convergence is equivalent to the property that, for any ε > 0, there are finitely many terms of the series such that excluding these terms results in a series with total sum less than the constant function ε, and this property does not refer to the ordering.

References

↑ Kiyosi Itō (1987). Encyclopedic Dictionary of Mathematics, MIT Press.