Uncertainty theory
Uncertainty theory is a branch of mathematics based on normality, monotonicity, self-duality, countable subadditivity, and product measure axioms. It was founded by Baoding Liu [1] in 2007 and refined in 2009.[2]
Mathematical measures of the likelihood of an event being true include probability theory, capacity, fuzzy logic, possibility, and credibility, as well as uncertainty.
Five axioms
Axiom 1. (Normality Axiom) 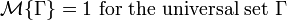 .
.
Axiom 2. (Monotonicity Axiom) 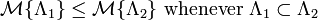 .
.
Axiom 3. (Self-Duality Axiom) 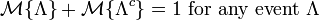 .
.
Axiom 4. (Countable Subadditivity Axiom) For every countable sequence of events Λ1, Λ2, ..., we have
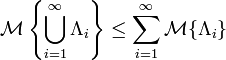 .
.
Axiom 5. (Product Measure Axiom) Let 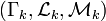 be uncertainty spaces for
be uncertainty spaces for 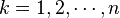 . Then the product uncertain measure
. Then the product uncertain measure 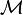 is an uncertain measure on the product σ-algebra satisfying
is an uncertain measure on the product σ-algebra satisfying
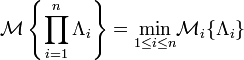 .
.
Principle. (Maximum Uncertainty Principle) For any event, if there are multiple reasonable values that an uncertain measure may take, then the value as close to 0.5 as possible is assigned to the event.
Uncertain variables
An uncertain variable is a measurable function ξ from an uncertainty space 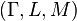 to the set of real numbers, i.e., for any Borel set B of real numbers, the set
to the set of real numbers, i.e., for any Borel set B of real numbers, the set
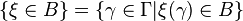 is an event.
is an event.
Uncertainty distribution
Uncertainty distribution is inducted to describe uncertain variables.
Definition:The uncertainty distribution ![\Phi(x):R \rightarrow [0,1]](../I/m/111a66c8ad3deba6e3e930ac8981f090.png) of an uncertain variable ξ is defined by
of an uncertain variable ξ is defined by 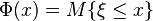 .
.
Theorem(Peng and Iwamura, Sufficient and Necessary Condition for Uncertainty Distribution) A function ![\Phi(x):R \rightarrow [0,1]](../I/m/111a66c8ad3deba6e3e930ac8981f090.png) is an uncertain distribution if and only if it is an increasing function except
is an uncertain distribution if and only if it is an increasing function except 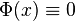 and
and 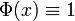 .
.
Independence
Definition: The uncertain variables 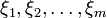 are said to be independent if
are said to be independent if
for any Borel sets 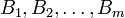 of real numbers.
of real numbers.
Theorem 1: The uncertain variables 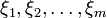 are independent if
are independent if
for any Borel sets 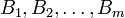 of real numbers.
of real numbers.
Theorem 2: Let 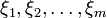 be independent uncertain variables, and
be independent uncertain variables, and 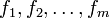 measurable functions. Then
measurable functions. Then 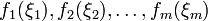 are independent uncertain variables.
are independent uncertain variables.
Theorem 3: Let 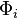 be uncertainty distributions of independent uncertain variables
be uncertainty distributions of independent uncertain variables 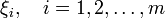 respectively, and
respectively, and 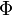 the joint uncertainty distribution of uncertain vector
the joint uncertainty distribution of uncertain vector 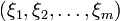 . If
. If 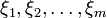 are independent, then we have
are independent, then we have
for any real numbers 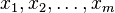 .
.
Operational law
Theorem: Let 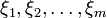 be independent uncertain variables, and
be independent uncertain variables, and 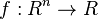 a measurable function. Then
a measurable function. Then 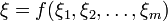 is an uncertain variable such that
is an uncertain variable such that
where 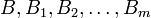 are Borel sets, and
are Borel sets, and 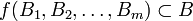 means
means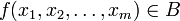 for any
for any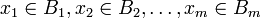 .
.
Expected Value
Definition: Let  be an uncertain variable. Then the expected value of
be an uncertain variable. Then the expected value of  is defined by
is defined by
provided that at least one of the two integrals is finite.
Theorem 1: Let  be an uncertain variable with uncertainty distribution
be an uncertain variable with uncertainty distribution 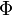 . If the expected value exists, then
. If the expected value exists, then
![E[\xi]=\int_0^{+\infty}(1-\Phi(x))dx-\int_{-\infty}^0\Phi(x)dx](../I/m/4ad88bdee5187c99bc96c9ad339ed932.png) .
.
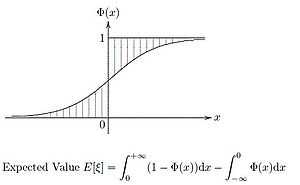
Theorem 2: Let  be an uncertain variable with regular uncertainty distribution
be an uncertain variable with regular uncertainty distribution 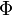 . If the expected value exists, then
. If the expected value exists, then
![E[\xi]=\int_0^1\Phi^{-1}(\alpha)d\alpha](../I/m/c582acb4d985e5f838a9c3fcae7a6cdb.png) .
.
Theorem 3: Let  and
and 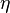 be independent uncertain variables with finite expected values. Then for any real numbers
be independent uncertain variables with finite expected values. Then for any real numbers 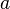 and
and 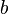 , we have
, we have
![E[a\xi+b\eta]=aE[\xi]+b[\eta]](../I/m/1bd1996a9c074c5b644482d544b31ca5.png) .
.
Variance
Definition: Let  be an uncertain variable with finite expected value
be an uncertain variable with finite expected value  . Then the variance of
. Then the variance of  is defined by
is defined by
![V[\xi]=E[(\xi-e)^2]](../I/m/1746eb406f832334f9ebdac4906ce839.png) .
.
Theorem: If  be an uncertain variable with finite expected value,
be an uncertain variable with finite expected value, 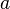 and
and 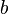 are real numbers, then
are real numbers, then
![V[a\xi+b]=a^2V[\xi]](../I/m/58560bbfbb2912baf08d3d14492a7ccd.png) .
.
Critical value
Definition: Let  be an uncertain variable, and
be an uncertain variable, and ![\alpha\in(0,1]](../I/m/a20ad44a15374ffd41728fbd75899830.png) . Then
. Then
is called the α-optimistic value to  , and
, and
is called the α-pessimistic value to  .
.
Theorem 1: Let  be an uncertain variable with regular uncertainty distribution
be an uncertain variable with regular uncertainty distribution 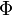 . Then its α-optimistic value and α-pessimistic value are
. Then its α-optimistic value and α-pessimistic value are
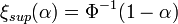 ,
,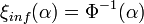 .
.
Theorem 2: Let  be an uncertain variable, and
be an uncertain variable, and ![\alpha\in(0,1]](../I/m/a20ad44a15374ffd41728fbd75899830.png) . Then we have
. Then we have
- if
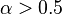 , then
, then 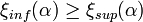 ;
; - if
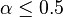 , then
, then 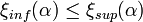 .
.
Theorem 3: Suppose that  and
and 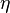 are independent uncertain variables, and
are independent uncertain variables, and ![\alpha\in(0,1]](../I/m/a20ad44a15374ffd41728fbd75899830.png) . Then we have
. Then we have
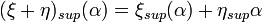 ,
,
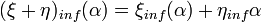 ,
,
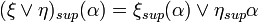 ,
,
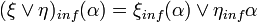 ,
,
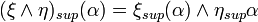 ,
,
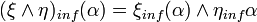 .
.
Entropy
Definition: Let  be an uncertain variable with uncertainty distribution
be an uncertain variable with uncertainty distribution 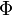 . Then its entropy is defined by
. Then its entropy is defined by
where 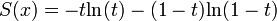 .
.
Theorem 1(Dai and Chen): Let  be an uncertain variable with regular uncertainty distribution
be an uncertain variable with regular uncertainty distribution 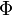 . Then
. Then
![H[\xi]=\int_0^1\Phi^{-1}(\alpha)\mbox{ln}\frac{\alpha}{1-\alpha}d\alpha](../I/m/49c978309a96c03da01cf99bfa5e16fd.png) .
.
Theorem 2: Let  and
and 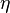 be independent uncertain variables. Then for any real numbers
be independent uncertain variables. Then for any real numbers 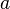 and
and 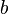 , we have
, we have
![H[a\xi+b\eta]=|a|E[\xi]+|b|E[\eta]](../I/m/c8d323c30b0ba0d1507867c412c504c0.png) .
.
Theorem 3: Let  be an uncertain variable whose uncertainty distribution is arbitrary but the expected value
be an uncertain variable whose uncertainty distribution is arbitrary but the expected value  and variance
and variance 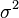 . Then
. Then
![H[\xi]\leq\frac{\pi\sigma}{\sqrt{3}}](../I/m/7dc0d8cd666800255eac3f2913993f2d.png) .
.
Inequalities
Theorem 1(Liu, Markov Inequality): Let  be an uncertain variable. Then for any given numbers
be an uncertain variable. Then for any given numbers 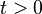 and
and 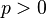 , we have
, we have
![M\{|\xi|\geq t\}\leq \frac{E[|\xi|^p]}{t^p}](../I/m/e046a131a3843627ba0a826cbb2ffa8e.png) .
.
Theorem 2 (Liu, Chebyshev Inequality) Let  be an uncertain variable whose variance
be an uncertain variable whose variance ![V[\xi]](../I/m/8232e3d17f1eea4e9a4a0770f81e9330.png) exists. Then for any given number
exists. Then for any given number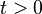 , we have
, we have
![M\{|\xi-E[\xi]|\geq t\}\leq \frac{V[\xi]}{t^2}](../I/m/de850f0f17d65b26aa6a56dcd6bbcf88.png) .
.
Theorem 3 (Liu, Holder’s Inequality) Let 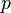 and
and 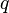 be positive numbers with
be positive numbers with 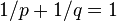 , and let
, and let  and
and 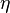 be independent uncertain variables with
be independent uncertain variables with ![E[|\xi|^p]< \infty](../I/m/11487b46691f80fc5900338f5e73a342.png) and
and ![E[|\eta|^q] < \infty](../I/m/7c8a36cacc1c7fdfc54afb97c9b1a068.png) . Then we have
. Then we have
![E[|\xi\eta|]\leq \sqrt[p]{E[|\xi|^p]} \sqrt[p]{E[\eta|^p]}](../I/m/2057ae295c705f7e28e47f51929ec50e.png) .
.
Theorem 4:(Liu [127], Minkowski Inequality) Let 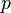 be a real number with
be a real number with 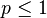 , and let
, and let  and
and 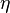 be independent uncertain variables with
be independent uncertain variables with ![E[|\xi|^p]< \infty](../I/m/11487b46691f80fc5900338f5e73a342.png) and
and ![E[|\eta|^q] < \infty](../I/m/7c8a36cacc1c7fdfc54afb97c9b1a068.png) . Then we have
. Then we have
![\sqrt[p]{E[|\xi+\eta|^p]}\leq \sqrt[p]{E[|\xi|^p]}+\sqrt[p]{E[\eta|^p]}](../I/m/849d1421275276e6151312cd73e0d5b6.png) .
.
Convergence concept
Definition 1: Suppose that 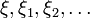 are uncertain variables defined on the uncertainty space
are uncertain variables defined on the uncertainty space 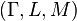 . The sequence
. The sequence 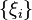 is said to be convergent a.s. to
is said to be convergent a.s. to  if there exists an event
if there exists an event 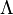 with
with 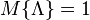 such that
such that
for every 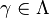 . In that case we write
. In that case we write 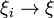 ,a.s.
,a.s.
Definition 2: Suppose that 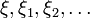 are uncertain variables. We say that the sequence
are uncertain variables. We say that the sequence 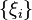 converges in measure to
converges in measure to  if
if
for every 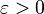 .
.
Definition 3: Suppose that 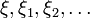 are uncertain variables with finite expected values. We say that the sequence
are uncertain variables with finite expected values. We say that the sequence 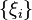 converges in mean to
converges in mean to  if
if
![\mbox{lim}_{i\rightarrow\infty}E[|\xi_i-\xi|]=0](../I/m/35869cc4f7fbd26c401b35a468e43d7a.png) .
.
Definition 4: Suppose that 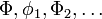 are uncertainty distributions of uncertain variables
are uncertainty distributions of uncertain variables 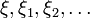 , respectively. We say that the sequence
, respectively. We say that the sequence 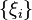 converges in distribution to
converges in distribution to  if
if 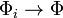 at any continuity point of
at any continuity point of 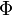 .
.
Theorem 1: Convergence in Mean 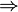 Convergence in Measure
Convergence in Measure 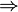 Convergence in Distribution.
However, Convergence in Mean
Convergence in Distribution.
However, Convergence in Mean  Convergence Almost Surely
Convergence Almost Surely  Convergence in Distribution.
Convergence in Distribution.
Conditional uncertainty
Definition 1: Let 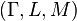 be an uncertainty space, and
be an uncertainty space, and 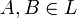 . Then the conditional uncertain measure of A given B is defined by
. Then the conditional uncertain measure of A given B is defined by
Theorem 1: Let 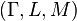 be an uncertainty space, and B an event with
be an uncertainty space, and B an event with 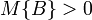 . Then M{·|B} defined by Definition 1 is an uncertain measure, and
. Then M{·|B} defined by Definition 1 is an uncertain measure, and 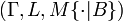 is an uncertainty space.
is an uncertainty space.
Definition 2: Let  be an uncertain variable on
be an uncertain variable on 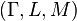 . A conditional uncertain variable of
. A conditional uncertain variable of  given B is a measurable function
given B is a measurable function 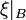 from the conditional uncertainty space
from the conditional uncertainty space 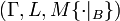 to the set of real numbers such that
to the set of real numbers such that
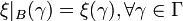 .
.
Definition 3: The conditional uncertainty distribution ![\Phi\rightarrow[0, 1]](../I/m/81b3150555bb3427d785cb630a338e66.png) of an uncertain variable
of an uncertain variable  given B is defined by
given B is defined by
provided that 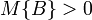 .
.
Theorem 2: Let  be an uncertain variable with regular uncertainty distribution
be an uncertain variable with regular uncertainty distribution 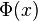 , and
, and 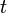 a real number with
a real number with 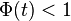 . Then the conditional uncertainty distribution of
. Then the conditional uncertainty distribution of  given
given 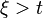 is
is
Theorem 3: Let  be an uncertain variable with regular uncertainty distribution
be an uncertain variable with regular uncertainty distribution 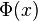 , and
, and 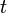 a real number with
a real number with 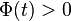 . Then the conditional uncertainty distribution of
. Then the conditional uncertainty distribution of  given
given 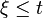 is
is
Definition 4: Let  be an uncertain variable. Then the conditional expected value of
be an uncertain variable. Then the conditional expected value of  given B is defined by
given B is defined by
provided that at least one of the two integrals is finite.
References
- ↑ Baoding Liu, Uncertainty Theory, 2nd ed., Springer-Verlag, Berlin, 2007.
- ↑ Baoding Liu, Uncertainty Theory, 4th ed., http://orsc.edu.cn/liu/ut.pdf.
- Xin Gao, Some Properties of Continuous Uncertain Measure, International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, Vol.17, No.3, 419-426, 2009.
- Cuilian You, Some Convergence Theorems of Uncertain Sequences, Mathematical and Computer Modelling, Vol.49, Nos.3-4, 482-487, 2009.
- Yuhan Liu, How to Generate Uncertain Measures, Proceedings of Tenth National Youth Conference on Information and Management Sciences, August 3–7, 2008, Luoyang, pp. 23–26.
- Baoding Liu, Some Research Problems in Uncertainty Theory, Journal of Uncertain Systems, Vol.3, No.1, 3-10, 2009.
- Yang Zuo, Xiaoyu Ji, Theoretical Foundation of Uncertain Dominance, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 827–832.
- Yuhan Liu and Minghu Ha, Expected Value of Function of Uncertain Variables, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 779–781.
- Zhongfeng Qin, On Lognormal Uncertain Variable, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 753–755.
- Jin Peng, Value at Risk and Tail Value at Risk in Uncertain Environment, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 787–793.
- Yi Peng, U-Curve and U-Coefficient in Uncertain Environment, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 815–820.
- Wei Liu, Jiuping Xu, Some Properties on Expected Value Operator for Uncertain Variables, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 808–811.
- Xiaohu Yang, Moments and Tails Inequality within the Framework of Uncertainty Theory, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 812–814.
- Yuan Gao, Analysis of k-out-of-n System with Uncertain Lifetimes, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 794–797.
- Xin Gao, Shuzhen Sun, Variance Formula for Trapezoidal Uncertain Variables, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 853–855.
- Zixiong Peng, A Sufficient and Necessary Condition of Product Uncertain Null Set, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 798–801.
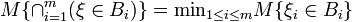
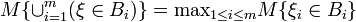
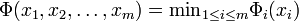
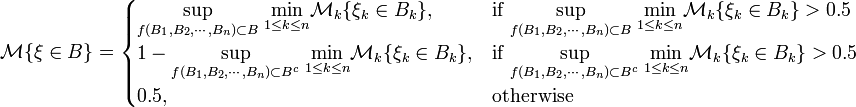
![E[\xi]=\int_0^{+\infty}M\{\xi\geq r\}dr-\int_{-\infty}^0M\{\xi\leq r\}dr](../I/m/4acefaa4ff23e180c09b33f108cd9d48.png)
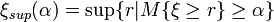
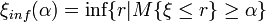
![H[\xi]=\int_{-\infty}^{+\infty}S(\Phi(x))dx](../I/m/baf65dcc46ef68511a6cf25e174bae58.png)
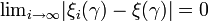
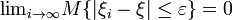
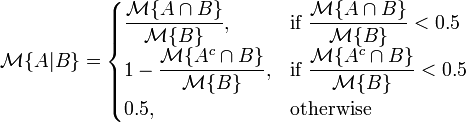
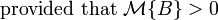
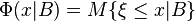
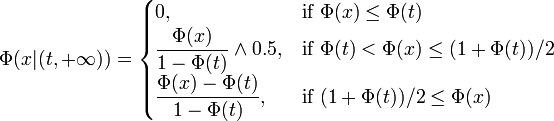
![\Phi(x\vert(-\infty,t])=\begin{cases} \displaystyle\frac{\Phi(x)}{\Phi(t)}, & \text{if }\Phi(x)\le\Phi(t)/2 \\ \displaystyle\frac{\Phi(x)+\Phi(t)-1}{\Phi(t)}\or 0.5, & \text{if }\Phi(t)/2\le\Phi(x)<\Phi(t) \\ 1, & \text{if }\Phi(t)\le\Phi(x) \end{cases}](../I/m/55030488f0a0dddea69dacd8a179a9bf.png)
![E[\xi|B]=\int_0^{+\infty}M\{\xi\geq r|B\}dr-\int_{-\infty}^0M\{\xi\leq r|B\}dr](../I/m/db46d421caea53e2498bd705e17bac63.png)