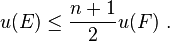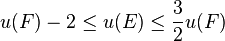u-invariant
In mathematics, the universal invariant or u-invariant of a field describes the structure of quadratic forms over the field.
The universal invariant u(F) of a field F is the largest dimension of an anisotropic quadratic space over F, or ∞ if this does not exist. Since formally real fields have anisotropic quadratic forms (sums of squares) in every dimension, the invariant is only of interest for other fields. An equivalent formulation is that u is the smallest number such that every form of dimension greater than u is isotropic, or that every form of dimension at least u is universal.
Examples
- For the complex numbers, u(C) = 1.
- If F is quadratically closed then u(F) = 1.
- The function field of an algebraic curve over an algebraically closed field has u ≤ 2; this follows from Tsen's theorem that such a field is quasi-algebraically closed.[1]
- If F is a nonreal global or local field, or more generally a linked field, then u(F) = 1,2,4 or 8.[2]
Properties
- If F is not formally real then u(F) is at most
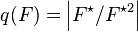 , the index of the squares in the multiplicative group of F.[3]
, the index of the squares in the multiplicative group of F.[3] - u(F) cannot take the values 3, 5, or 7.[4] Fields exist with u = 6[5][6] and u = 9.[7]
- Merkurjev has shown that every even integer occurs as the value of u(F) for some F.[8] [9]
- The u-invariant is bounded under finite-degree field extensions. If E/F is a field extension of degree n then
In the case of quadratic extensions, the u-invariant is bounded by
and all values in this range are achieved.[10]
The general u-invariant
Since the u-invariant is of little interest in the case of formally real fields, we define a general u-invariant to be the maximum dimension of an anisotropic form in the torsion subgroup of the Witt ring of F, or ∞ if this does exist.[11] For non-formally real fields, the Witt ring is torsion, so this agrees with the previous definition.[12] For a formally real field, the general u-invariant is either even or ∞.
Properties
- u(F) ≤ 1 if and only if F is a Pythagorean field.[12]
References
- ↑ Lam (2005) p.376
- ↑ Lam (2005) p.406
- ↑ Lam (2005) p. 400
- ↑ Lam (2005) p. 401
- ↑ Lam (2005) p.484
- ↑ Lam, T.Y. (1989). "Fields of u-invariant 6 after A. Merkurjev". Ring theory 1989. In honor of S. A. Amitsur, Proc. Symp. and Workshop, Jerusalem 1988/89. Israel Math. Conf. Proc. 1. pp. 12–30. Zbl 0683.10018.
- ↑ Izhboldin, Oleg T. (2001). "Fields of u-Invariant 9". Annals of Mathematics, 2 ser 154 (3): 529–587. Zbl 0998.11015.
- ↑ Lam (2005) p. 402
- ↑ Elman, Karpenko, Merkurjev (2008) p. 170
- ↑ Mináč, Ján; Wadsworth, Adrian R. (1995). "The u-invariant for algebraic extensions". In Rosenberg, Alex. K-theory and algebraic geometry: connections with quadratic forms and division algebras. Summer Research Institute on quadratic forms and division algebras, July 6-24, 1992, University of California, Santa Barbara, CA (USA). Proc. Symp. Pure Math. 58.2. Providence, RI: American Mathematical Society. pp. 333–358. Zbl 0824.11018.
- ↑ Lam (2005) p. 409
- ↑ 12.0 12.1 Lam (2005) p. 410
- Lam, Tsit-Yuen (2005). Introduction to Quadratic Forms over Fields. Graduate Studies in Mathematics 67. American Mathematical Society. ISBN 0-8218-1095-2. MR 2104929. Zbl 1068.11023.
- Rajwade, A. R. (1993). Squares. London Mathematical Society Lecture Note Series 171. Cambridge University Press. ISBN 0-521-42668-5. Zbl 0785.11022.
- Elman, Richard; Karpenko, Nikita; Merkurjev, Alexander (2008). The algebraic and geometric theory of quadratic forms. American Mathematical Society Colloquium Publications 56. American Mathematical Society, Providence, RI. ISBN 978-0-8218-4329-1.