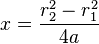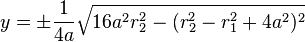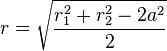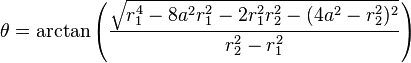Two-center bipolar coordinates

For related concepts, see Bipolar coordinates.

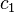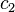In mathematics, two-center bipolar coordinates is a coordinate system, based on two coordinates which give distances from two fixed centers, c_1 and c_2.[1] This system is very useful in some scientific applications (e.g. calculating the electric field of a dipole on a plane).[2][3]

Transformation to Cartesian coordinates

Cartesian coordinates and polar coordinates.

The transformation to Cartesian coordinates 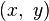(x,\ y) from two-center bipolar coordinates 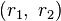(r_1,\ r_2) is

x = \frac{r_2^2-r_1^2}{4a}
y = \pm \frac{1}{4a}\sqrt{16a^2r_2^2-(r_2^2-r_1^2+4a^2)^2}

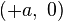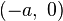where the centers of this coordinate system are at (+a,\ 0) and (-a,\ 0).[1]

Transformation to polar coordinates

When x>0 the transformation to polar coordinates from two-center bipolar coordinates is

r = \sqrt{\frac{r_1^2+r_2^2-2a^2}{2}}
\theta = \arctan \left(\frac{\sqrt{r_1^4-8a^2r_1^2-2r_1^2r_2^2-(4a^2-r_2^2)^2}}{r_2^2-r_1^2} \right)\,\!

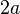where 2 a is the distance between the poles (coordinate system centers).

See also

References

  1. ↑ 1.0 1.1 Weisstein, Eric W., "Bipolar coordinates", MathWorld.
  2. ↑ R. Price, The Periodic Standing Wave Approximation: Adapted coordinates and spectral methods.
  3. ↑ The periodic standing-wave approximation: nonlinear scalar fields, adapted coordinates, and the eigenspectral method.