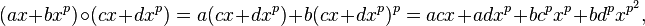Twisted polynomial ring
In mathematics, a twisted polynomial is a polynomial over a field of characteristic  in the variable
in the variable  representing the Frobenius map
representing the Frobenius map 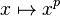 . In contrast to normal polynomials, multiplication of these polynomials is not commutative, but satisfies the commutation rule
. In contrast to normal polynomials, multiplication of these polynomials is not commutative, but satisfies the commutation rule
for all  .
.
Over an infinite field, the twisted polynomial ring is isomorphic to the ring of additive polynomials, but where multiplication on the latter is given by composition rather than usual multiplication. However, it is often easier to compute in the twisted polynomial ring — this can be applied especially in the theory of Drinfeld modules.
Definition
Let  be a field of characteristic
be a field of characteristic  . The twisted polynomial ring
. The twisted polynomial ring 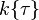 is defined as the set of polynomials in the variable
is defined as the set of polynomials in the variable  and coefficients in
and coefficients in  . It is endowed with a ring structure with the usual addition, but with a non-commutative multiplication that can be summarized with the relation
. It is endowed with a ring structure with the usual addition, but with a non-commutative multiplication that can be summarized with the relation 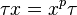 . Repeated application of this relation yields a formula for the multiplication of any two twisted polynomials.
. Repeated application of this relation yields a formula for the multiplication of any two twisted polynomials.
As an example we perform such a multiplication
Properties
The morphism
defines a ring homomorphism sending a twisted polynomial to an additive polynomial. Here, multiplication on the right hand side is given by composition of polynomials. For example
using the fact that in characteristic  we have the Freshman's dream
we have the Freshman's dream 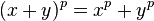 .
.
The homomorphism is clearly injective, but is surjective if and only if  is infinite. The failure of surjectivity when
is infinite. The failure of surjectivity when  is finite is due to the existence of non-zero polynomials which induce the zero function on
is finite is due to the existence of non-zero polynomials which induce the zero function on  (e.g.
(e.g. 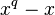 over the finite field with
over the finite field with  elements).
elements).
Even though this ring is not commutative, it still possesses (left and right) division algorithms.
References
- Goss, D. (1996), Basic structures of function field arithmetic, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)] 35, Berlin, New York: Springer-Verlag, ISBN 978-3-540-61087-8, MR 1423131, Zbl 0874.11004
- Rosen, Michael (2002), Number Theory in Function Fields, Graduate Texts in Mathematics 210, Springer-Verlag, ISBN 0-387-95335-3, ISSN 0072-5285, Zbl 1043.11079
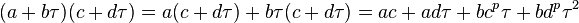
![k\{\tau\}\to k[x],\quad a_0+a_1\tau+\cdots+a_n\tau^n\mapsto a_0x+a_1x^p+\cdots+a_nx^{p^n}](../I/m/0b1294f0e29faf2f09bea37179a23cf1.png)