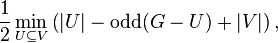Tutte–Berge formula

In the mathematical discipline of graph theory the Tutte–Berge formula, named after William Thomas Tutte and Claude Berge, is a characterization of the size of a maximum matching in a graph. It is a generalization of Tutte's theorem.

The theorem states that the size of a maximum matching of a graph G = (V, E) equals

where odd(H) is the number of components in the graph H with an odd number of vertices.

See also

• Hall's theorem
• Tutte's theorem

References

• Berge, C. (1958). "Sur le couplage maximum d'un graphe". Comptes rendus hebdomadaires des séances de l'Académie des sciences 247: 258–259. 
• Bondy, J. A.; Murty, U. S. R. (2007). Graph theory: an advanced course. Graduate Texts in Mathematics. Springer-Verlag. p. 428. ISBN 1-84628-969-6. 
• Bondy, J. A.; Murty, U. S. R. (1976). Graph Theory with Applications. New York: North Holland. ISBN 0-444-19451-7. 
• Brualdi, Richard A. (2006). Combinatorial matrix classes. Encyclopedia of Mathematics and Its Applications 108. Cambridge: Cambridge University Press. p. 360. ISBN 0-521-86565-4. Zbl 1106.05001. 
• Lovász, László; Plummer, M. D. (1986). Matching theory. Amsterdam: North-Holland. pp. 90–91. ISBN 0-444-87916-1. 
• Schrijver, Alexander (2003). Combinatorial optimization: polyhedra and efficiency. Springer-Verlag. p. 413. ISBN 3-540-44389-4. 
• Tutte, W. T. (1947). "The factorization of linear graphs". The Journal of the London Mathematical Society, Ser. 1 22 (2): 107–111. doi:10.1112/jlms/s1-22.2.107.