Turbo equalizer

In digital communications, a turbo equalizer is a type of receiver used to receive a message corrupted by a communication channel with intersymbol interference (ISI). It approaches the performance of a maximum a posteriori (MAP) receiver via iterative message passing between a soft-in soft-out (SISO) equalizer and a SISO decoder.^[1] It is related to turbo codes in that a turbo equalizer may be considered a type of iterative decoder if the channel is viewed as a non-redundant convolutional code. The turbo equalizer is different from classic a turbo-like code, however, in that the 'channel code' adds no redundancy and therefore can only be used to remove non-guassian noise.

History

Turbo codes were invented by Claude Berrou in 1990-1991. In 1993, turbo codes were introduced publicly via a paper listing authors Berrou, Glavieux, and Thitimajshima.^[2] In 1995 a novel extension of the turbo principle was applied to an equalizer by Douillard, Jézéquel, and Berrou.^[3] In particular, they formulated the ISI receiver problem as a turbo code decoding problem, where the channel is thought of as a rate 1 convolutional code and the error correction coding is the second code. In 1997, Glavieux, Laot, and Labat demonstrated that a linear equalizer could be used in a turbo equalizer framework.^[4] This discovery made turbo equalization computationally efficient enough to be applied to a wide range of applications.^[5]

Overview

Standard Communication System Overview

Before discussing turbo equalizers, it is necessary to understand the basic receiver in the context of a communication system. This is the topic of this section.

At the transmitter, information bits are encoded. Encoding adds redundancy by mapping the information bits $a$ to a longer bit vector – the code bit vector $b$ . The encoded bits $b$ are then interleaved. Interleaving permutes the order of the code bits $b$ resulting in bits $c$ . The main reason for doing this is to insulate the information bits from bursty noise. Next, the symbol mapper maps the bits $c$ into complex symbols $x$ . These digital symbols are then converted into analog symbols with an D/A converter. Typically the signal is then up-converted to pass band frequencies by mixing it with a carrier signal. This is a necessary step for complex symbols. The signal is then ready to be transmitted through the channel.

At the receiver, the operations performed by the transmitter are reversed to recover 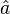$\hat{a}$ , an estimate of the information bits. The down-converter mixes the signal back down to baseband. The A/D converter then samples the analog signal, making it digital. At this point, $y$ is recovered. The signal $y$ is what would be received if $x$ were transmitted through the digital baseband equivalent of the channel plus noise. The signal is then equalized. The equalizer attempts to unravel the ISI in the received signal to recover the transmitted symbols. 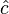It then outputs the bits $\hat{c}$ associated with those symbols. The vector 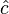$\hat{c}$ may represent hard decisions on the bits or soft decisions. If the equalizer makes soft decisions, it outputs information relating to the probability of the bit being a 0 or a 1. If the equalizer makes hard decisions on the bits, it quantizes the soft bit decisions and outputs either a 0 or a 1. Next, the signal is deinterleaved which is a simple permutation transformation that undoes the transformation the interleaver executed. Finally, the bits are decoded by the decoder. The decoder estimates 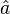$\hat{a}$ from $\hat{b}$ .

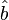A diagram of the communication system is shown below. In this diagram, the channel is the equivalent baseband channel, meaning that it encompasses the D/A, the up converter, the channel, the down converter, and the A/D.

Turbo Equalizer Overview

The block diagram of a communication system employing a turbo equalizer is shown below. The turbo equalizer encompasses the equalizer, the decoder, and the blocks in between.

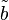The difference between a turbo equalizer and a standard equalizer is the feedback loop from the decoder to the equalizer. Due to the structure of the code, the decoder not only estimates the information bits $a$ , but it also discovers new information about the coded bits $b$ . The decoder is therefore able to output extrinsic information, $\tilde{b}$ about the likelihood that a certain code bit stream was transmitted. Extrinsic information is new information that is not derived from information input to the block. This extrinsic information is then mapped back into information about the transmitted symbols $x$ for use in the equalizer. 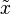These extrinsic symbol likelihoods, $\tilde{x}$ , are fed into the equalizer as a priori symbol probabilities. The equalizer uses this a priori information as well as the input signal $y$ to estimate extrinsic probability information about the transmitted symbols. 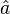The a priori information fed to the equalizer is initialized to 0, meaning that the initial estimate $\hat{a}$ made by the turbo equalizer is identical to the estimate made by the standard receiver. The information 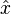$\hat{x}$ is then mapped back into information about $b$ for use by the decoder. The turbo equalizer repeats this iterative process until a stopping criterion is reached.

Turbo Equalization in Practical Systems

In practical turbo equalization implementations, an additional issue need to be considered. The channel state information (CSI) that the equalizer operates on comes from some channel estimation technique, and hence un-reliable. Firstly, in order to improve the reliability of the CSI, it is desirable to include the channel estimation block also into the turbo equalization loop, and parse soft or hard decision directed channel estimation within each turbo equalization iteration.^[6]^[7] Secondly, incorporating the presence of CSI uncertainty into the turbo equalizer design leads to a more robust approach with significant performance gains in practical scenarios.^[8]^[9]

References

↑ R. Koetter, A.C. Singer, and M. Tüchler Turbo Equalization IEEE Signal Processing Mag., vol. 21, no. 1, pp. 67–80, Jan. 2004.
↑ Berrou, Claude; Glavieux, Alain; Thitimajshima, Punya, Near Shannon Limit Error – Correcting International Conference on Communications, 1993.
↑ Douillard, Catherine; Jézéquel, Michel; Berrou, Claude, Iterative Correction of Intersymbol-Interference: Turbo-Equalization European Transactions on Telecommunications, vol. 6, no. 5, pp. 507-511, September–October 1995.
↑ A. Glavieux, C. Laot, and J. Labat, “Turbo equalization over a frequency selective channel,” in Proc. Int. Symp. Turbo Codes, Brest, France, Sept. 1997, pp. 96–102.
↑ M. Tüchler, R. Koetter, and A.C. Singer, “Turbo Equalization: Principles and New Results,” IEEE Transactions on Communications, vol. 50, no. 5, pp. 754-767, May 2002.
↑ M. Sandell, C. Luschi, P. Strauch, and R.Yan, “Iterative Data Detection and Channel Estimation for Advanced TDMA Systems,” IEEE GLOBECOM, Australia, pp. 3728–3733, Nov 1998.
↑ S. Y. Park and C. G. Kang, “Complexity-Reduced Iterative MAP Receiver for Interference Suppression in OFDM-Based Spatial Multiplexing Systems,” IEEE Transactions on Vehicular Technology, vol. 53, pp. 1316–1326, Sep 2004.
↑ M. Danish Nisar and Wolfgang Utschick. "Minimax Robust A-priori Information Aware Channel Equalization", in IEEE Transactions on Signal Processing, Volume 59, pp 1734 - 1745, April 2011.
↑ N. Kalantarova, S. S. Kozat, and A. T. Erdogan, “Robust Turbo Equalization Under Channel Uncertainties,” IEEE Transactions on Signal Processing, 2012.

External links

Turbo Equalization a Signal Processing Magazine primer on turbo equalization. Since it was written for the signal processing community in general, it is relatively accessible.
Turbo Equalization: Principles and New Results an IEEE Transactions on Communications journal article that offers a detailed, clear explanation of turbo equalization.